
| �z�[�� | �����T�v | ���ƃA�C�f�B�A | ���H���� | �Q�l���� | �������ƃg�b�v�� |
 |
||||||||||||||
|
||||||||||||||
| �w�K��� | �w���̃|�C���g | �֘A�̂���P�� | |
| ���̐}�̂悤�Ȓ����`�̍L����������܂��B���̍L�����̒Z���ӂ��A�P�Q�ɕ����钼�����K���g�킸�Ɍ����܂��傤�B �@�@  (�q���g) �E�������܂��Ă݂܂��傤�B �E���s���Ɛ����̔���g���܂��B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�E���ۂɁA�L�������������A�܂�Ȃ��銈����������Ȃ���w������B [��] 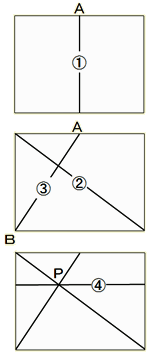 (�P)�܂��A���̐^�łQ�����ɐ܂��Ē����@������B (�Q)���ɁA�L���đΊp���A������B (�R)�܂��L���āA���x�́A�`�A�a��ʂ�悤�Ȓ����B������B (�S)�Ō�ɁA������x�L���āA�����A�ƒ����B�Ƃ̌�_�o��ʂ��Ē��ӂƕ��s�ɐ܂�ƒ����`�̏c���R�������钼���C���ł���B ���Ȃ��A�T�����������邱�Ƃ��ł���B |
�}�`�Ƒ��� (���R) |
|
�@ 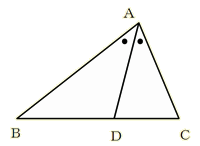 �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�E�⏕���̈�������ς��邱�ƂŁA�l�X�ȏؖ����ł��邱�Ƃ�������B [��] �y�ؖ����̂P�z �@�}�̂悤�ɁA���_�b��ʂ�A�����`�c�ɕ��s�Ȓ����������A�����a�`�Ƃ̌�_���o�Ƃ���B �`�c//�o�b������ �`�o���`�b �䂦�ɁA���s���̐������ 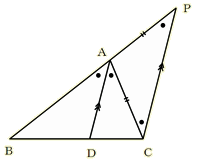 �`�a�F�`�b���`�a�F�`�o �`�a�F�`�b���`�a�F�`�o�@�@�@�@ �@���a�c�F�c�b �y�ؖ����̂Q�z �@�}�̂悤�ɓ_�c��ʂ�A�����`�b�ɕ��s�Ȓ����������A�����`�a�Ƃ̌�_���o�Ƃ���B 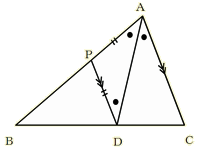 �`�a�F�`�b���a�o�F�o�c �@�@�@�@ �@���a�o�F�o�` �@�@�@�@�@ ���a�c�F�c�b �y�ؖ����̂R�z �@�}�̂悤�ɓ_�a��ʂ�����`�b�ɕ��s�Ȓ����������A�����`�c�Ƃ̌�_���o�Ƃ���B �`�b//�a�o������ �܂��A ����� �a�c�F�c�b���a�o�F�`�b�E�E�E�E�E�E�E�E�E�E�E�E(�P) �܂��A �`�a���a�o�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E(�Q) 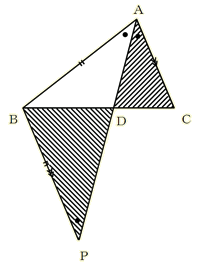 (�P)�A(�Q)��� �`�a�F�`�b���a�c�F�c�b �@�@�@�@�@�@�@�@�@ �y���̑��̕⏕���z �@ 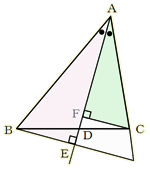 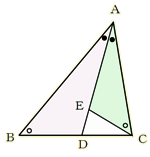 |
�}�`�Ƒ��� (���R) �}�`�Əؖ� (���Q) |
|
| �`�O���Ƃ́A�����ɐ܂��Ă��Ƃ̗p���Ƒ����ɂȂ钷���`�̒��Ŗʐς��P (�P)�`���̏c�Ɖ��̒����̔�����߂܂��傤�B (�Q)�`�S���̖ʐς����߂܂��傤�B (�R)�`�S���̏c�̒����A���̒������K�ő���A�c�Ɖ��̒����̔�A�ʐς��v�Z���A(�P)��(�Q)�̓����Ɣ�r���܂��傤�B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�E�R�N�́u�}�`�Ƒ����v���w�K������̔��W�I�ȓ��e�Ƃ��Ď�舵���B�g�߂ɂ���`���p���ɂ��āA��Ƃ�ώ@��ʂ��Ă��̋K�i�̂��܂�ׂĂ����B�ʐςƕӂ̒����̊W����A�����`�̏c�Ɖ��̒����̔���A��������p���ċ��߂�����B���l�̊W�ɂ�����̂Ƃ��āA�a���p���ɂ��Ă��Љ�邱�Ƃ��ł���B�܂��A�`�S���̑Ίp���̒������a�S���� 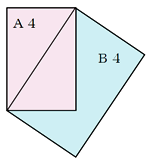 �����ӂ̒����ɓ������B �����ӂ̒����ɓ������B[��]  |
�}�`�Ƒ��� (���R) ������ (���R) |
|
| �������H������100�����ő���Ƃ��A�u���[�L��ł���Ԃ��~�܂�܂ł̒�~�����͂ǂꂭ�炢�ł��傤�B �@ �@ 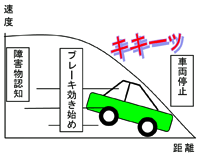 �@ 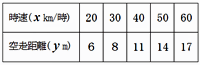 �@  �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�E�ۑ���u�����Ԃ̒�~���������߂�v�Ƃ��A����A�����ԖƋ����擾����ۂɕK�v�ƂȂ鎖����ݒ肵���B�܂��A��~�����������Ɛ��������ɕ����邱�ƂŁA�P�N�Ŋw�K�������ƁA�R�N�Ŋw�K������ �E���o�I�A���ϓI�Ɋ�����肳���邽�߂ɁA��~�����������Ɛ��������ɕ����A�����Ƃ���_�O���t��A�Ή��\�����B [��]  �@�@�@�ڂ����͂�������N���b�N���y���w�Z�@���H����z |
�� (���R) ���Ɣ���� (���P) |
| Copyright(C) 2008 SAGA Prefectural Education Center. All Rights Reserved. |