| ホーム | 研究概要 | 授業アイディア | 実践事例 | 参考資料 | 研究事業トップへ |
|
||||||||||||||
|
||||||||||||||
| 各学年のボタンをクリックしてください。 | |||
 |
 |
 |
 をクリックすると、授業で使えるワークシートがダウンロードできます。 |
| 学習問題 | 指導のポイント | 関連のある単元 | |
 に１〜９の数字を入れましょう。（に同じ数字が入ってもかまいません。） |
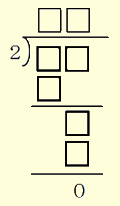・まず、 に入る数を自由に考えさせるが、問題の意味理解を深めるために、題意に当てはまらない場合を示す。・数通りの答えが出た後、 に入る数に何かきまりがないか考えさせる。・最後は、わる数が３や４の場合の問題作りにつなげてもよい。 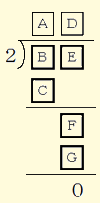 [解答例] (Ａ，Ｂ，Ｃ，Ｄ，Ｅ，Ｆ，Ｇ)＝(１，２，２，１，２，２，２)、(１，２，２，２，４，４，４）、…ＢＣＥＦＧには２の倍数し か入らない。 また、Ｂ＝Ｃ、Ｅ＝Ｆ＝Ｇになる、 などのきまりに気付かせたい。 |
わり算の筆算 (小４) |
|
2007年はいのしし年(亥年)です。2050年は何年でしょう。また、西暦１年は何年でしょう。 |
・2008年は子年、2009年は丑年、2010年は寅年、…というように1年ごとに変わっていくイメージをもたせる。 ・12年で一回りすることを確認し、わる数が12になること、余りの意味を考えさせる。 [解答例] 12年後、12年前がちょうど亥年になる。わり切れたら亥年。 2050年…43÷12＝３あまり７になり、2050から７をひいた2043年が亥年になる。よって2050年は午年になる。 西暦１年…2007÷12＝167あまり３になり、2007から３をひいた2004年前の西暦３年が亥年。よって西暦１年は酉年。 |
わり算の筆算 (小４) |
|
| (１)１円玉の直径は２cmです。１円玉を何枚ならべると100mの長さになるでしょう。 (２)１円玉を唐津市から佐賀市まで一列にならべていこうと思います。およそ50kmの道のりがあります。１円玉は何枚ならぶでしょう。 |
・１円玉の特徴(直径２cm、重さ１ｇ)を確認する。 ・10枚分で20cm、100枚分で200cm(２ｍ)…というように長さの既習事項について確認する。 ・ものさしが無い場合でも、身近な物を使えば、長さが表せることを知ることで、生活の中での活用に広げることができる。 [解答例] (１)5000枚 (２)250万枚 |
大きな数 (小４) わり算(小４) 長さ(小３) |
|
給食の牛乳パック約24枚でトイレットペーパーが１個できます。むつごろう小で10月に集めた牛乳パックで、トイレットペーパーは約何個できるでしょう。 |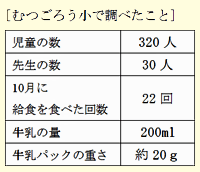
・給食の牛乳パック24枚でトイレットペーパーが１個できることを確認する。 ・10月に何枚の牛乳パックが集まったかが分かればいいことを確認する。 ・表から必要な条件のみを使って計算することを伝える。 ・余りを切り捨てることを実際の場面で考えさせる。 ・表を使った新たな問題作りをさせ、算数の活用場面を広げる。 [解答例] 式 (320＋30)×22÷24＝320あまり20 答え 320個 |
わり算(小４) かけ算(小３) |
|
下の図形の面積を求めました。式を見てどのように面積を求めたか図に表しましょう。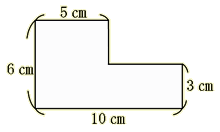 (１) ６×５＋３×５ (２) ３×10＋３×５ (３) ６×10−３×５ (４) (10＋５)×３ (５) (６＋３)×５ |
・まず、面積を求めさせる。解き方には触れず、面積が何  になるか確認する。・(１)から(５)までの式を基に図に補助線を入れさせて、式のもつ意味について意見を交流させる。 ・途中の式がどこの面積のことを表しているのか、確認しながらまとめる。 ・面積の学習を一通り終えた時期に、複合図形の求積の復習として位置付けたい。 [解答例]  |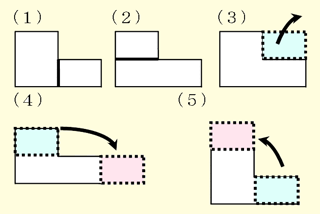
式と計算 (小４) 面積(小４) |
|
下のような箱を作りました。箱の面に色紙を切りばりして、かざりたいと思います。むだなく用意するには、何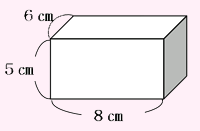の色紙があればいいでしょう。 |
・箱の形を思い出させ、各面の図形に注目させ、６つの長方形からできていることを確認する。 ・全体での学び合いの中で、２つずつ同じ形があり、×２で表すことができることを確認する。 ・終末に、「１ のタイルを敷きつめるとしたら何枚タイルが必要でしょう。」と問い掛け、面積を求めることは１の正方形がいくつ分かを求めるということを再認識させる。・「牛乳パックで立方体を作り色紙をはる」という場面を考えさせ、活用場面を広げる。 [解答例] ・各面の面積を求めてたす。 40＋40＋30＋30＋48＋48＝236 ・同じ面が２面ずつあるので２倍してたす。 40×２＋30×２＋48×２＝236 ・どの面も２面ずつあるのでまとめて２倍する。 (40＋30＋48)×２＝236 詳しくはこちらをクリック→【小学校 実践事例】 |
面積(小４) 式と計算 (小４) はこの形 (小３) |
|
(１)１辺が10ｃｍの正方形の色紙３枚を下のようにならべたときの面積を求めましょう。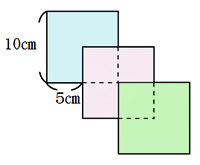 (２)10枚重ねたときの面積を求めましょう。 |
・実際の正方形の用紙を図のように４分の１ずつずらしてはり合わせながら提示し、問題場面をとらえさせる。 ・いろいろな求め方を出し合わせることで、同じ面積を求めるのに幾通りものやり方があることを確認する。 ・４枚のとき、５枚のとき、･･･の面積の変わり方を表にまとめさせる。 ・表からきまりがあることに気付かせる。 [解答例] (１) 250 (２) 775 |
面積(小４) 変わり方 (小４) 式と計算 (小４) |
|
三角定規を組み合わせて120°を作りましょう。 |
・三角定規の角を組み合わせることで角度を作ることができることを確認する。 ・一組の三角定規を用い、90°＋30°で作ることができることを一人一人実際に操作しながら共通理解する。 ・グループで同形の三角定規も数枚使って120°を作ることができないか考えを出し合い、発表させる。 ・他の角(例えば150°、160°、…)なども作ることができないか、活用場面を広げる。 [解答例] 90＋30、60＋60、60＋30＋30、45＋45＋30、… |
角の大きさ (小４) 式と計算 (小４) |
|
運動場に長さが20ｍのひもで長方形または正方形の遊び場を作ります。一番面積が大きくなるのは、たてと横の長さがそれぞれ何ｍのときでしょう。 |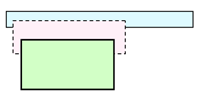
・周りの長さが同じでも、広さ(面積)が違うことを、実際に数値に当てはめて考えさせることにより、再確認する。 ・変わり方に着目させるために、辺の長さと面積の関係を表にまとめる。 ・辺の長さと面積の関係を調べる活動を通して、面積の意味理解を深めさせる。 [解答例] 一辺が５ｍの正方形になるとき。 |
変わり方 (小４) 面積(小４) 式と計算 (小４) |
| Copyright(C) 2008 SAGA Prefectural Education Center. All Rights Reserved. |
