| ■ 学年別指導案の例(高校3年生) |
| 1.単元名 : 数学Ⅰ・数学A・数学Ⅱ・数学B |
| 2.対 象:高校3年生 |
| 3.教材内容について |
| (1)教材観 図形については,これまでいろいろな図形の性質について,様々な角度から様々な方法を用いて説明することにより,問題解決につなげる方法を学んできた。 今回の指導では,一般に機械的な理解に終始しやすいチェバの定理,メネラウスの定理を例に,改めて初等幾何学のよさを味わわせるとともに,これまでに学んだ図形学習を踏まえ,論理的に図形を考察できるようにしていく。 将来の図形学習に必要な思考力・応用力の育成に直結するものであり,丁寧に扱いたい教材である。 (2)指導観 生徒は,図形の性質を知識としては知っているが,その根拠となる考え方を正しく理解し,条件を示しながら説明できる生徒は少ない。 学習状況調査結果においても,一定の理解度を示すのにもかかわらず,学年が進むにつれて,既習の学習内容を活用し,最も適当な解法を見いだし問題解決を行う能力を発揮できていない実態がある。 こうしたことから,「角の二等分線」を発展させ,条件を変えたり,一般化したりする作業を通して,論理的に考えるよさを身に付けさせる必要がある。 また,これまで学んだ内容が,図形問題の解決に有効であることを理解させ,数学的思考力を更に向上させたいと考える。 (3)単元の目標 図形の性質を論理的に説明することができ,問題を様々な方法で考察したり,解決したりする能力を養う。 |
| 4.指導計画 |
| 数学Ⅰ,数学A,数学Ⅱ,数学Bのまとめ(計15時間) (1)数学Ⅰ・数学A・・・・・・・平面図形,図形と計量の復習(5時間) (2)数学Ⅱ・数学B・・・・・・・図形と方程式,三角関数,平面ベクトルの復習(10時間) 本時3/10 |
| 5. 本時の指導 |
| (1)本時の目標 チェバの定理,メネラウスの定理を三角形の頂角の二等分線や中線及び垂線の交点で成り立つことを確認する過程を通して一般化し,数学的思考力を高める。 (2)本時の学習指導過程 |
| 過程 | 主な学習活動 | 指導上の留意点 | 評価活動等 |
導 入 |
・ 本時のねらいを説明する。 ・ 既習事項を確認する。 角の二等分線の性質 メネラウスの定理 チェバの定理 |
・性質を形式的に暗記するだけでなく,いろいろな証明法やその考え方を問題解決に結び付けるように指導する。 | 【知識・理解】 角の二等分線の性質や与えられた定理を正しく理解できる。 |
| 展 開 |
・① 3辺の長さが与えられた三角形の各頂角の二等分線を作図し,チェバの定理が成り立つことを確かめる。 【チェバの定理】 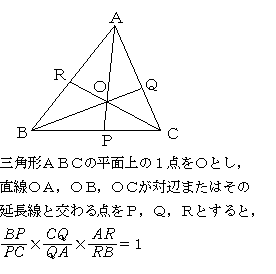 ・ 中線の交点(重心)を通るとき成り立つことを確かめる。 ・ チェバの定理が「角の二等分線」の 交点O(内心)を通るとき成り立つことを証明する。 (例)  →BC=a ,CA=b,AB=cとして証明。 ・② 頂角から対辺に下ろした垂線を作図し垂心Oを通るとき,チェバの定理が成り立つことを証明する。 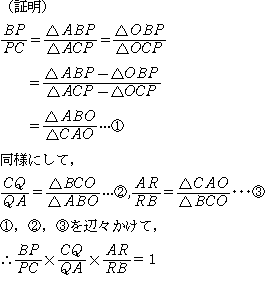 ・ 三角形の傍心Oを通るとき成り立つことを確かめる。 |
・指導計画を示し,明らかに成り立つ「中線」の事例をはじめとして,段階的に解決していくことを確認させる。 ・点Oが三角形の外部にあっても成り立つことを補足する。 ・線分の比を三角形の面積比で表せることに留意するよう指導する。 ・ 三角形平面上の任意の点一般化して証明できることを指導する。 ・点Oが三角形の外部にあるときも,成り立つことを指導する。 ・余力のある生徒には,点Aを始点とする位置ベクトルを用いた証明方法を考えてみるように指導する。 |
【知識・理解】 角の二等分線の性質を図形の計量に活用できる。 【知識・理解】 三角形の面積比が理解でき,証明に活用できる。 |
| ま と め |
・1つの課題がいろいろな方法で論理的に解決できることを確認する。 |
・自分で条件をきちんと整理しながら,問題解決の方法を振り返るように指導する。 | |
| ■ 他学年の指導案↓ |
| 中学校1年 | 中学校2年 | 中学校3年 | 高 校1年 | 高 校2年 | 高 校3年 |