| 仭 妛擭暿巜摫埬偺椺乮崅峑侾擭惗乯 |
| 侾丏扨尦柤丗悢妛俙丂暯柺恾宍丆悢妛嘥丂恾宍偲寁検 |
| 俀丏懳丂徾:崅峑侾擭惗 |
| 俁丏嫵嵽偵偮偄偰 |
| 丂嶰妏宍偺捀妏偺擇摍暘慄偺挿偝傪丆偙傟傑偱偺妛廗撪梕傪妶梡偟懡條側曽朄偱媮傔傞丅 |
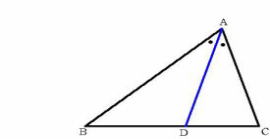 |
| 乮侾乯嫵嵽娤 丂恾宍偺寁検偵偮偄偰偼丆拞妛峑俁擭惗偱乽憡帡偺峫偊傪妶梡偱偒傞偙偲乿丆乽嶰暯曽偺掕棟偺堄枴傪棟夝偟偦傟傪妶梡偱偒傞偙偲乿偑栚昗偲偟偰帵偝傟偰偍傝丆恎偺夞傝偺傕偺偺應掕偵妶梡偱偒傞偙偲偑媮傔傜傟偰偄傞丅偝傜偵丆崅摍妛峑侾擭惗偱偼丆嶰妏斾傪應検偵妶梡偱偒傞偙偲偑媮傔傜傟偰偍傝丆掕宆揑側夝朄偵偮偄偰偼挌擩側巜摫偑側偝傟偰偄傞丅 丂偟偐偟丆壽戣夝寛擻椡偺岦忋傪恾傞偨傔偵偼丆婛廗帠崁偺桳梡惈傪堄幆偟丆恾宍偵嫽枴傪傕偮傛偆側巜摫偺廩幚偑偝傜偵媮傔傜傟偰偄傞丅 丂杮嫵嵽偼丆乽嶰妏宍偺捀妏偺擇摍暘慄偺挿偝傪媮傔傞乿夁掱傪捠偟偰丆偙傟傑偱妛傫偩恾宍偺徹柧摍偺撪梕偑偳偆惗偐偝傟偰偄傞偺偐棟夝偱偒傞傕偺偱偁傞丅曗彆慄傪棙梡偟偨婔壗揑夝朄偺桳梡惈偑妋擣偱偒傞偲偲傕偵丆惗搆偺敪憐傪朙偐偵偱偒傞嫵嵽偱偁傞偲峫偊傞丅 乮俀乯巜摫娤 丂偙傟傑偱偼丆暯柺恾宍偲偦偺惈幙偵偮偄偰丆庬乆偺掕棟傗徹柧傪屄暿偵妛傫偱偒偨丅墘廗傪捠偟偰丆栤戣偺夝朄傪尒晅偗偨傝丆岞幃偲偟偰妶梡偟偨傝偡傞偙偲偼偱偒傞傕偺偺丆懱宯揑偵徹柧傪埵抲偯偗偨傝丆峫偊曽傪扨尦傪墇偊偰妶梡偡傞偙偲傪妛傇婡夛偼彮側偄丅 丂杮帪偺僥乕儅偼丆嶰妏宍偺捀妏偺擇摍暘慄偺挿偝傪媮傔傞拞偱丆婛廗偺夝朄埲奜偵暋悢偺夝朄傪峫偊偝偣傞乽悢妛揑妶摦乿傪庢傝擖傟偨庼嬈偲偡傞丅 丂暯峴慄傗悅慄側偳偺揔摉側曗彆慄傪堷偔弶摍婔壗揑側夝朄傗丆嵗昗暯柺傪棙梡偡傞夝愅婔壗傪梡偄傞曽朄側偳丆懡條側夝朄傪巜摫偡傞拞偱丆偲傝傢偗弶摍婔壗偺傕偮僔儞僾儖偝傗桳岠惈傪嵞妋擣偝偣傞偲偲傕偵丆懡條偵峫偊傞偙偲偺偡偽傜偟偝傪枴傢傢偣偨偄丅 丂崅摍妛峑偵偍偗傞恾宍妛廗偺愡栚偺帪婜偵丆婛廗帠崁傪懱宯揑偵怳傝曉傞偲偲傕偵丆恾宍偵嫽枴傪傕偨偣傞巜摫傪庢傝擖傟傞偙偲偼丆崱屻偺妛廗妶摦偵桳岠偱偁傞偲峫偊傞丅 |
| 係丏巜摫寁夋 |
| 丂丂悢妛俙丂戞俁復丂暯柺恾宍丂丂丂丂丂 侾俆帪娫 丂丂悢妛嘥丂戞係復丂恾宍偲寁検丂丂丂丂 俀係帪娫 丂丂悢妛俙丂戞侾復丂廤崌偲榑棟丂 丂丂丂丂俆帪娫 丂丂杮帪 |
| 俆丏杮帪偺巜摫 |
| 乮侾乯杮帪偺巜摫栚昗丒昡壙婯弨 丂嘆妏偺擇摍暘慄偺惈幙傪棟夝偡傞偲偲傕偵丆恾宍偺寁検偵妶梡偱偒傞丅亂抦幆丒棟夝亃 丂嘇栤戣夝寛偵偼丆暋悢偺徹柧曽朄偑偁傞偙偲偵娭怱傪傕偪丆帺傜庢傝慻傕偆偲偡傞丅 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亂娭怱丒堄梸丒懺搙亃 乮俀乯杮帪偺妛廗巜摫夁掱 |
| 仭丂懠妛擭偺巜摫埬伀 |
| 拞妛峑侾擭 | 拞妛峑俀擭 | 拞妛峑俁擭 | 崅丂峑侾擭 | 崅丂峑俀擭 | 崅丂峑俁擭 |