|
||||
| 実施日:平成17年12月9日(金) | ||||
|
対象者: 佐賀県立致遠館高等学校 理数科1年(40名) |
|||
|
授業者: 佐賀県教育センター研究員 牟田久俊 |
|||
| 1.単元 |
| 単元:数学A 平面図形,数学Ⅰ 図形と計量,数学Ⅱ 図形と方程式 |
| 2.指導計画(使用教科書:東京書籍 数学Ⅰ・数学A・数学Ⅱ) ※ 本時の関連分野のみ |
| 数学A 第3章 平面図形 15時間 |
| 数学Ⅰ 第4章 図形と計量 24時間 |
| 数学A 第1章 集合と論理 5時間 |
| 数学Ⅱ 第1章 方程式・式と証明 27時間 |
| 数学Ⅱ 第2章 図形と方程式 21時間(本時17/21) |
| 3.本時の題材 | 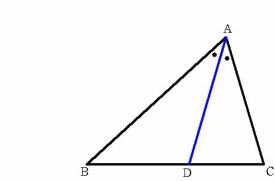 |
| 三角形の頂角の二等分線の長さを,これまでの学習内容を活用し多様な方法で求める。 |
| 5.本時の学習指導 |
| (1)本時の指導目標・評価規準 |
| ①角の二等分線の性質を理解するとともに,図形の計量に活用できる。【知識・理解】 ②問題解決には,複数の証明方法があることに関心をもち,自ら取り組もうとする。 【関心・意欲・態度】 |
| (2)本時の学習指導過程 |
| 指導過程 | 主な学習活動 |
指導上の留意点 評価の観点 |
評価 活動 |
| 【導入】 (10分) 角の二等分線の 性質を証明法を 通して振り返る。 プレゼンテーション教材 ワークシート1(PDF) |
・与えられた△ABCの頂角の二等分線を作図し, ・BD:DC=AB:AC を証明する方法を振り返る。  (方法1)平行線分の比の性質を利用 (方法2)面積を利用 (方法3)補助円を利用 等 |
・これまでに学んだ具体的な証明問題を振り返る中で,理解度を確認しながら関心をもたせる。 【関心・意欲・態度】 ①角の二等分線の性質を理解し,作図の意味を説明することができる。 ②相似形や平行線分の比の性質を理解し,図形の計量に活用できる。 ③具体的な事象の数量関係を三角比などを用いて表現し,図形の計量に活用できる。 ④正弦定理や余弦定理を図形の計量に活用できる。 ⑤三角形の面積を用いて,図形の計量ができる。 ⑥図形を座標平面上に表すことによって,図形の計量ができる。 以上のように複数の考え方ができることを確認し,図形の解法に生かせることを指導する。 |
【関心・意欲・態度】 複数の証明方法があることに関心をもち,自ら取り組もうとする。 |
| 【展開】 ワークシート2(PDF) (35分) (1)課題の把握 (2)解決方法の予想 (3)自分の考えの説明(発表) (4)解決方法の確認 |
問1 AB=6,AC=10,∠BAC=120°を満たす△ABCの角Aの二等分の長さADを様々な方法で求めよう。 (生徒発表例) ・「面積」を利用して求める。 △ABC=△ABD+△ADCより 1/2AB・ACSin120°=1/2AB・AD ・Sin60°+1/2AD・ACSin60° ・平行な補助線を用いて考える。 (1)点Cを通りADに平行な直線CPを引く。 (2)点Bを通りADに平行な直線BPを引くなど。 ・相似な三角形を作図して考える。 ・補助円を用いて考える。 ・「座標平面」を利用して求める。 (1)点Aを原点にとり,Cをx軸上にとる。 (2)点Aを原点にとり,Bをx軸上にとる。 その他の解法を説明する。 出てきた考え方を分類・整理する。 |
・生徒が考えた解法を板書し,その根拠や手順を発表する。 ・論に至る推論の過程を筋道を立てて説明できるように留意する。 ・中線定理と混同しないよう留意する。 ・前日に課題プリントを配付し,基本的な解法は教科書・ノート等で確認するように指導する。 ・自由な発想がスムースにできるよう生徒が自らの手で計算したり,解決できる問題を既習事項の中から出題していることを知らせ,自分で回答の確認ができるよう指導する。 ・証明の思考過程で用いた考え方が問題解決に有用であることを確認する。 ・生徒の発表で出てこなかった解法について指導する。 ・それぞれの解法が理解できる。 【数学的な見方・考え方】 |
【知識・理解】 面積を利用する方法で,証明することができる。 【知識・理解】 補助線を引いて,証明を考えることができる。 |
| (5)課題の一般化 (拡張) (6)解決方法の確認 |
問2 AB=a,AC=b,∠BAC=2θ°を満たす△ABCの角Aの二等分の長さADを求めよう。  ・どのような考え方をすればいいか考える。 ・問1と同じ考え方でできるのではないかと予想する。 ・ADに平行な補助線を引く方法で考える。 (1)ADに平行な直線CPを引く (2)ADに平行な直線BPを引く など。 ・相似な三角形を作図する方法で考える。 ・垂線を引く方法で考える。 出てきた解法以外の説明を簡単に行う。 これまでの考え方をまとめる。 |
・既習事項の振り返りの大切さに気付かせる。 【数学的な見方考え方】 ・それぞれ,△ACD,△ ABDが二等辺三角形になることに気付かせる。 ・問1の解法を一般化する過程にも応用できることを理解させる。 ・思考過程を大切にすることを指導する。 |
|
| 【まとめ】 (10分) |
今日の課題を考える過程で出た考えを整理し,それぞれの特徴やよかったところを考えてみる。 | ・生徒に自己評価を行わせ,本日の学習内容を確認させる。 ・自己評価シート(PDF)の配布 |
| 6 研究授業の記録 |
| 研究授業の記録 | ||
| 1 授業前の生徒の意識調査(PDF)結果 (一部抜粋) |
||
| 実施日時:平成17年12月9日(金)授業後 | ||
| 対象生徒:致遠館高校理数科1年生 | ||
 |
 |
|
| <分析1> | <分析2> | |
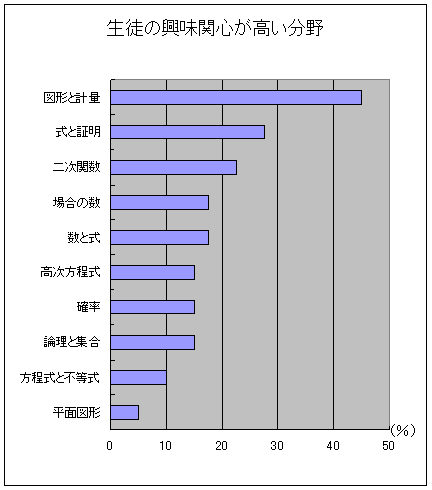
| 授業前は,生徒が興味・関心をもっている分野として,記憶に新しい「図形と計量」,「式と証明」「二次関数」などが上位にきている。 本時に取り扱う「平面図形」については,最も関心が低く4.5%の生徒が回答したにとどまった。 |
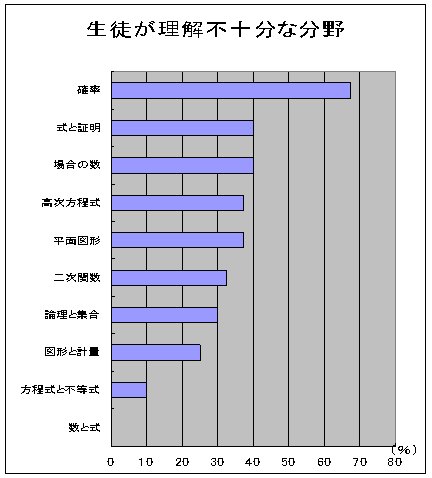
授業前は,生徒が理解不十分な分野として,「確率」,「式十証明」,「場合の数」などが上位にきている。 本時に取り扱う「平面図形」については,37.5%の生徒が回答しており,全体の中位にあった。 |
|
| ■アンケートの結果から,生徒は「図形と計量」や「式と証明」など手法がある程度決まっている分野には,興味・関心をもって取り組む。理数科の生徒にとっては,「平面図形」に関しては,それほど理解が不十分である分野とは考えていないにもかかわらず,興味・関心は低い。 研究授業では,こうした意識を変化させるような,教材を提示するとともに,生徒に数学的活動を体験させることを通して,「平面図形」への興味・関心を高めていきたいと考えた。 |
||
| 2 授業後の生徒の自己評価結果 | ||
|
実施日時:平成17年12月9日(金)研究授業終了後 |
||
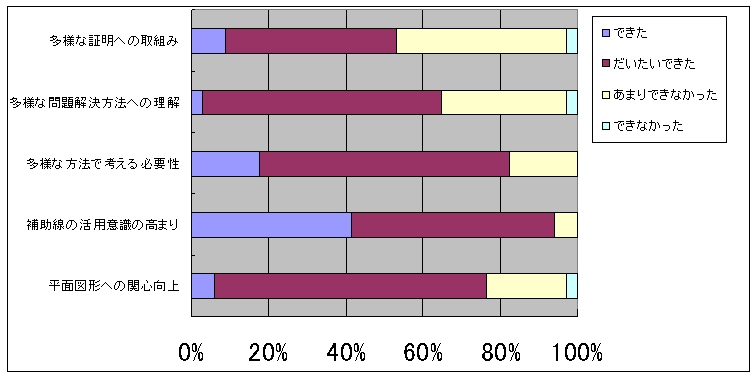 |
||
| 質 問 内 容 | コ メ ン ト | |
|
(質問1) |
研究授業の前日配付し,課題としていた証明問題については,「できた」,「だいたいできた」を合わせ53%の生徒が自分なりに取り組めたと考えている。クラスの生徒のほとんどが,2種類程度の方法で証明できていたことから,「あまりできなかった」「不十分だ」と解答した生徒の多くは,授業で紹介した多数の証明法や「ピタゴラスの定理」の300を超える証明法の多さに驚き,相対的に自己評価がやや厳しい結果となったものと考えられる。 | |
| (質問2) 「角の二等分線の長さ」の解法を自分なりにいろいろ 考えることができましたか |
「できた」,「だいたいできた」を合わせ65%の生徒が自分なりに取り組めたと考えている。全員に指定した「三角形の面積を利用する解法」は,ほとんどの生徒が正答しており,別解についても自分なりに考えることができ,おおむね取り組めたと評価している。 | |
|
(質問3) |
「できた」,「だいたいできた」を合わせ82%の生徒が理解できたと考えている。 自由記述でも,1つの問題にたくさんの切り口で証明できたり,問題解決ができたりすることに驚いたという記述が多く,多様な方法で考える必要性を理解している。 |
|
|
(質問4) |
「思う」,「少しは思うようになった」を合わせ94%の生徒が支持している。 |
|
| (質問5) 平面図形と身近なことがらの関連に気付き,平面図形へ の関心が高くなりましたか。 |
「高くなった」,「少しは高くなった」を合わせ76%の生徒が支持している。 理数科の生徒で日ごろから関心が高い中で,授業の導入等で日常生活に関連のある内容に触れることによって,より一層,意識の高まりがみられた。 |
|
| 7 研究授業の感想及び仮説の検証 |
| (1)生徒の感想 | ||
|