| ■ | 研究授業の記録(画像) | ||
| 導入 | 角の二等分線のいろいろな証明方法をプレゼンテーションソフトで説明しました。 | ||
| 展開 | 角の二等分線の長さをいろいろな方法で求めています。 | ||
| ○ADに平行な補助線を引いてみた | ○ADに垂直な補助線ではどうかな | ○外接円をかいて考えてみよう | |
| ■ | 研究授業の記録(概要) |
| 【本時の授業のねらいについて】 今日の授業のテーマは,「いろいろな発想法」。 現在の科学技術は「いろいろな発想」があって「進歩」につながっている。 「いろいろな発想法」について,図形でよく目にする「角の二等分線」を題材として多くの考え方に触れ,自分自身で考えてもらいたい。 |
|
| 【導入】(数学と社会のつながりについて) 例:デジタルカメラの「手ぶれ防止装置」の手法について。 →各社のカメラやレンズ等の条件によって開発手法に違いがあることを説明。 1つの技術でもいろいろな方法が開発されており,その背景に、数学や理科の基礎科学の研究の積み重ねがある。 ピタゴラスの定理の証明法も約360通りあることが知られている。 皆さんも将来の科学者の卵として,本日の授業を通して,いろいろな方法を考える習慣を養ってほしい。 <問1>角の二等分線の比の性質について(復習) △ABCの内角の二等分線と比の定理の証明 ・・・・プレゼンテーションソフトで説明 ・生徒に前日配付したプリント(宿題)をもとに,目的をもって補助線を引く方法を指導しながら解説を進める。 → 補助線の引き方によって,いろいろな考え方ができることを確認させる。 |
|
| 【展開】 (問2)θ=120°の場合の二等分線の長さを求めさせる。 (1)全員に共通課題として「三角形の面積」を用いる解法を指定する。 また,グループ毎に以下の中から「解法」を選択し指定する。 ① 平行な補助線(ヒント:相似な三角形を見付ける) ② 垂直な補助線(ヒント:相似な直角三角形を見付ける) ③ 正弦定理・余弦定理 ④ 補助円(外接円など)(ヒント:相似な三角形を見付ける) (2)各自、答案を作らせる。 →必ず,作図をして考えるよう指導する。 (時間があれば,3つ以上の解法を考えておくように指示する) (3)グループの中から代表を指名し,板書の上,発表させる。 |
|
| 【まとめ】<いろいろな考えがあり,それが今後の学習の役に立つことを振り返らせる> ・問題解決に当たって,別の考え方が大変役に立つ。 ・社会への還元事例 →カメラのレンズの焦点距離の2とおりの作図法について (a)光の性質(直進性、屈折)による作図【物理的作図法】 (b)角(120°)の二等分線の長さを利用した作図【数学的作図法】 ※生徒の自己評価(配付) |
|
| ■ 角の二等分線の性質のいろいろな証明 | |
定 理 |
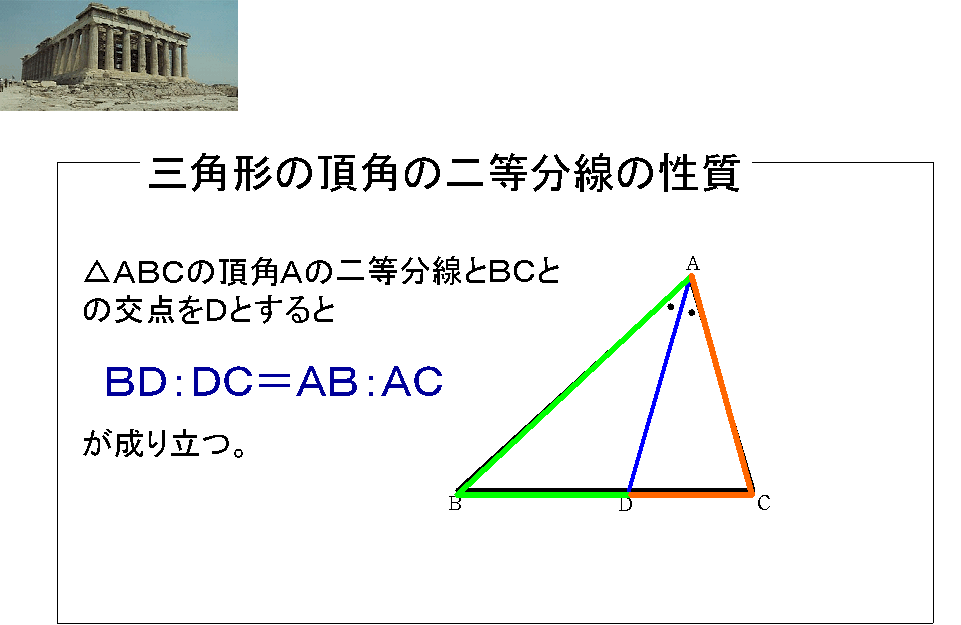 |
証 明 1 |
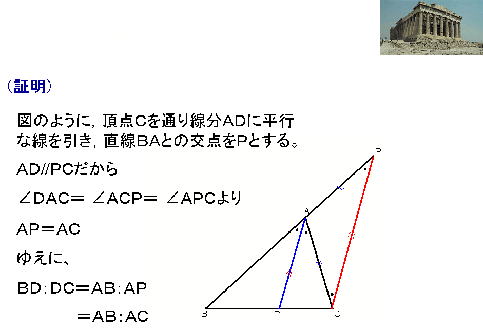 |
証 明 2 |
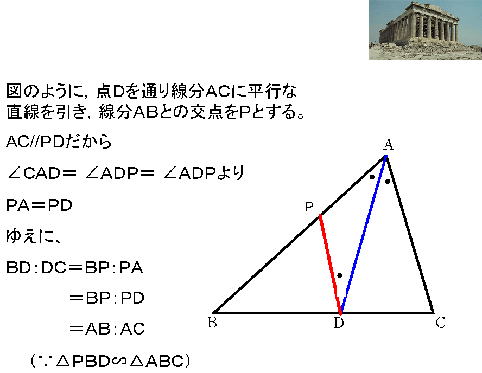 |
証 明 3 |
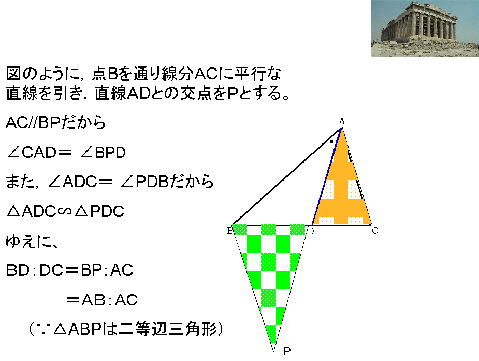 |
証 明 4 |
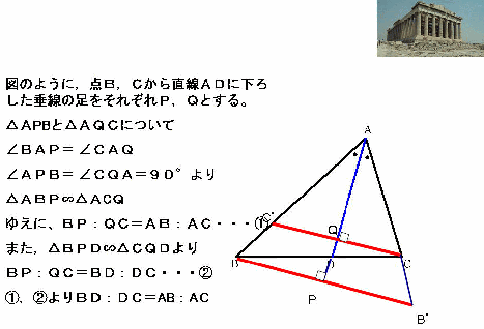 |
証 明 5 |
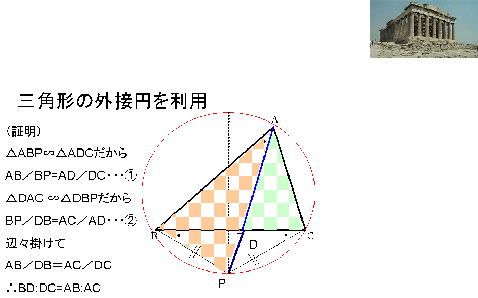 |
証 明 6 |
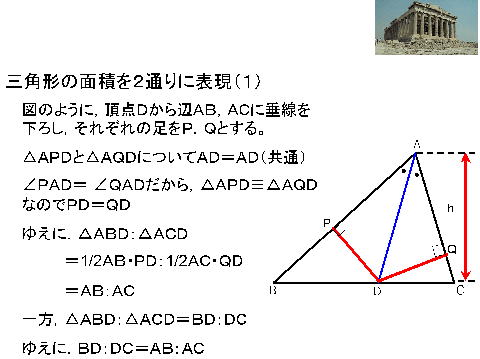 |
証 明 7 |
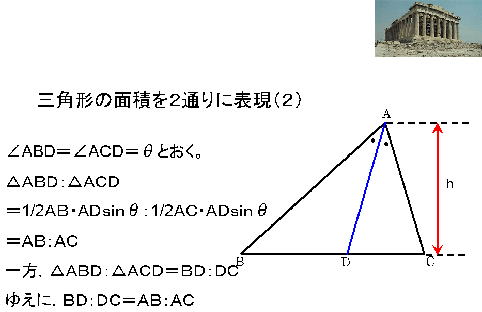 |
| 補 助 線 の 引 き 方 |
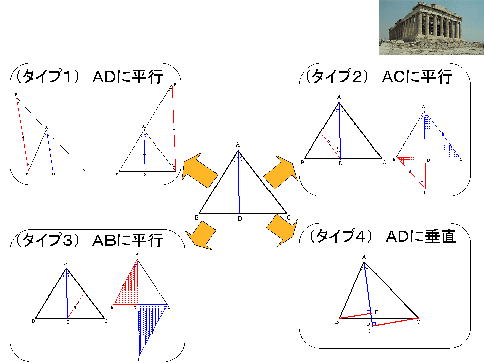 |
| 他にも,三角形の外接円・内接円などの補助円や,座標平面等を用いる証明法があり,30通り以上あります。 | |
| ■生徒の解答例(角の二等分線の性質の証明) | |
| 自宅で生徒に課題として与えた結果,それぞれのタイプ毎の傾向は次のようになった。(解答数延べ33名) | |
| タイプ1(ADに平行な補助線)・・・・14名 タイプ2(ACに平行な補助線)・・・・ 1名 タイプ3(ABに平行な補助線)・・・・ 5名 タイプ4(ADに垂直な補助線)・・・・ 0名 タイプ5(三角形の面積利用)・・・・ 7名 タイプ6(補助円の利用)・・・・・・・・ 0名 誤答・無答・・・・・・・・・・・・・・・・・・・ 6名 |
|
| (分析) | |
| 教科書には,ADに平行な補助線を利用された証明法が採用されており,多くの生徒はこの証明法で理解していたと思われる。次いで,面積で証明できる生徒が多かった。垂直な補助線や補助円については,授業で指導する機会がほとんどないため,思いつかなかったと思う。今後は,様々な方法を紹介して,問題に適した証明ができるように指導する必要がある。 また,補助線を引く目的やその手法についても,機会を設けて指導していく必要性を感じた。 |
|
| ■生徒の解答例(角の二等分線の長さ) | |
| ○角の二等分線の性質の証明で紹介した手法を用いて,「角の二等分線の長さ」を求める。 まず、三角比の授業で学習した「面積を用いる方法」で全員が解答した。 →机間指導で数人の生徒には助言・指導する必要があったが,最終的にはほとんど全員が正解していた。 |
|
| 次にその他の手法に挑戦し,代表者が発表した。 生徒が思いついた方法は次のようになった。 タイプa(ADに平行な補助線を引く方法) タイプb(点BからACの延長に垂線を引く方法) タイプc(ADを延長し点Cから垂線を引く方法) タイプd(余弦定理を利用する方法) タイプe(三角形ABCの外接円を利用する方法) |
|
| (分析) | |
| 様々な方法を紹介した後であり,生徒はいろいろな方法で取り組むようになった。 こちらが予想した以上に,バラエティに富んだ解答が出てきており,本時は十分な時間を与えることができなかったため,こうした授業では,時間を十分用意すべきであったと反省した。2時間以上は必要な内容であった。 |
|