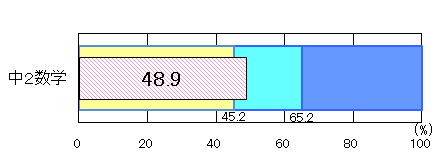
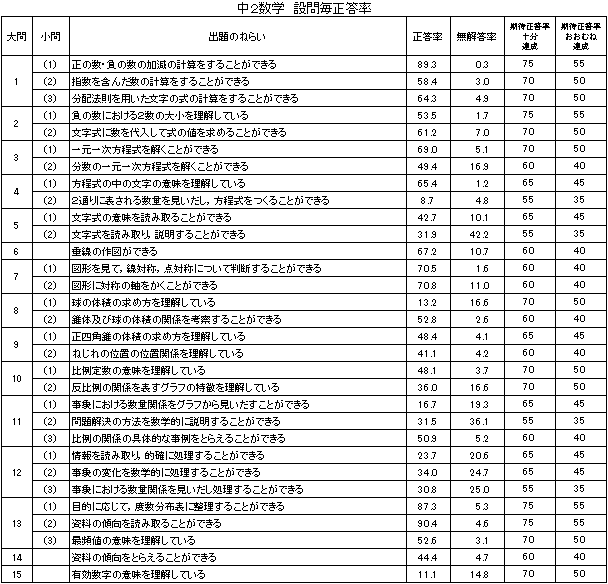
「数と式」、「関数」の領域における「活用」に関する問題の正答率が低く、無解答率が高い。
[中学2年生 大問4の(2)]
○ 問題の概要
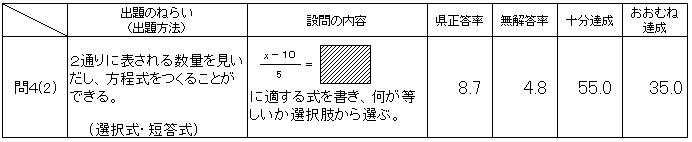
○ 解答状況
正答率は8.7と、「おおむね達成」の期待正答率35.0を大きく下回った。与えられた情報の中から、数量の関係を的確に読み取り、式に表すという数学的な思考力に大きな課題がある。
○ 指導法改善の手立て
この問題は、まず2つの未知数が問われており、未知数 x の置き方によって2通りの方程式が考えられるものであった。太郎さんの考え(生徒の人数をxとおいて、お菓子の数が等しいことに目を付ける)が一般的であると思うが、花子さんの考え(お菓子の数を x とおいて、生徒の数が等しいことに目を付ける)も理解できるような柔軟な思考力を身に付けさせたいものである。授業においても、このような2通り以上の考え方ができる方程式の問題等を題材として取り扱うことにより、数学的な思考力を培うこともできると考える。
[中学2年生 大問5の(1),(2)]
○ 問題の概要
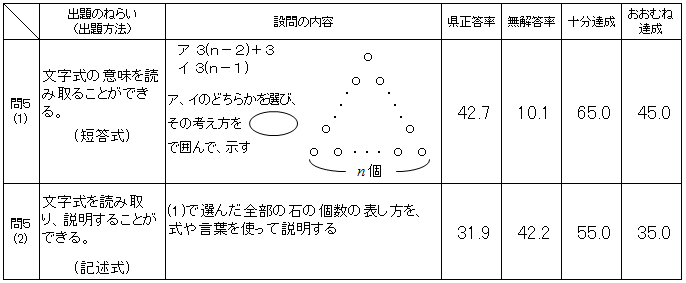
○ 解答状況
(1)は「おおむね達成」の期待正答率45.0に対し正答率は42.7、(2)は「おおむね達成」の期待正答率35.0に対し正答率は31.9で、ともに下回った。特に(2)については、無解答率も42.2と高い数値であった。文字式の意味を読み取ったり説明したりするために必要となる数学的な思考力・表現力において課題が見られた。
○ 指導法改善の手立て
ある具体的な数量について表された文字式の意味を読み取ったり、逆に具体的な数量を一般化して文字式に表す場合については、幅広い視野での数学的な見方や考え方が必要になる。さらに、(2)のように説明を必要とする場合については、数学的な表現力や言語能力も必要となる。このような問題については、主に課題学習の中で取り扱われることが多いが、図を用いたり数を数えたりするところから、規則性や数量の関係に気付かせ、文字式として一般化させていくような取り組みが大切である。そういった活動を通して、幅広い視野での数学的な思考力が培われていくものと考える。また授業の中で、自分が予想したことやその理由等について、書き表したり人に伝えたりする活動も合わせて取り組むことによって、数学的な表現力や言語能力が培われていくものと考える。
[中学2年生 大問11の(1),(2)]
○ 問題の概要
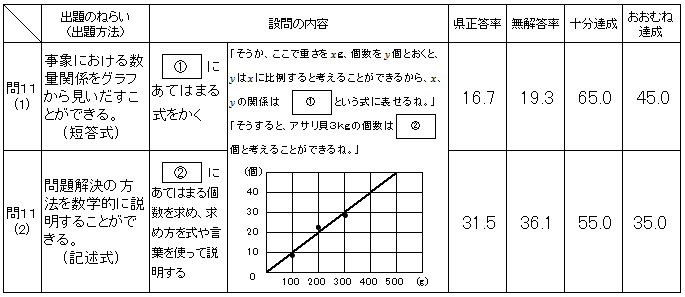
○ 解答状況
(1)は「おおむね達成」の期待正答率45.0に対し正答率は16.7、(2)は「おおむね達成」の期待正答率35.0に対し正答率は31.5で、ともに下回った。さらに無解答率については、(1)が19.3、(2)が36.1と高い数値であった。事象を数学化する力や、数学的に解釈したり表現したりする力に課題が見られた。
○ 指導法改善の手立て
この問題においては、比例にかかわる基礎的・基本的な知識・技能と、それらを活用する力が求められている。特に比例や反比例を学習するにあたっては、できるだけ身近にあるような題材を用いて、分かりやすいものから取り扱い、基礎的・基本的な知識・技能の定着を図りながら、少しずつ思考力を伴うような問題へとステップアップしていく進め方がよいと考える。また、正答率が低かった原因の一つとして、目盛りの違うx軸とy軸のグラフの見方や考え方について、慣れていなかったことも考えられる。教科書においては、このような題材の取り扱いも少ないため、別に題材や課題を提示して、そこから思考力や表現力をはぐくむような学習活動を取り入れていく必要がある。
[中学2年生 大問12の(1),(2),(3)]
○ 問題の概要

○ 解答状況
「おおむね達成」の期待正答率は(1)45.0、(2)45.0、(3)35.0であったが、正答率は(1)23.7、(2)34.0、(3)30.8と、すべて下回った。無解答率も、(1)20.6、(2)24.7、(3)25.0と高い数値を示した。情報を読み取り活用する力や、事象の変化をとらえ、数学的に処理する力などにおいて、課題が見られた。
○ 指導法改善の手立て
(1)については、多くの与えられた情報の中から数量の関係(x、yの関係)を見いだす力が求められている。また、(2)、(3)については、与えられた情報を整理して見る力と、そこから見い出される数量の関係を的確に読み取り、それらを活用していく力が求められている。一つの単元や関連内容の学習が終了する節目となる時間に、このような問題を取り扱った授業を実践することは、数学的な思考力・表現力を高める上においても、基礎的・基本的な知識・技能の定着を図る上においても大きな効果をもたらすものと考える。実践にあたっては、題材や課題の提示、場面の設定などの工夫が大切である。
|