平成23年度の中学２年生における正答率は、「おおむね達成」の基準を下回った。正答率を評価の観点別に見ると、３つの観点全てにおいて「おおむね達成」の基準を下回り、特に「数学的な見方や考え方」の正答率が低い結果であった。内容・領域別に見ると、「数と式」は「おおむね達成」の基準を上回ったが、他の内容・領域は下回った。設問別に見ると、問題解決の方法や考え方をことばや式を使って説明するような「活用」に関する問題が「おおむね達成」の基準を下回り、また、数学の用語や記号に関わる内容や、グラフ上の点を座標に表すことなど基礎的・基本的な問題についても、「おおむね達成」の基準を下回り、課題が見られた。さらに、平成22年度調査からの課題であった学習指導要領の移行に伴い新しく追加された内容についても、課題が見られる結果となった。今後の指導に当たっては、「知識・技能の定着」と「知識・技能を活用できるような数学的な思考力・判断力・表現力の育成」の、双方を意図した学習過程の見直しと授業の改善が大切である。特に、課題解決の方法などを説明し伝え合うような活動（言語活動に関わる数学的活動）を意図的に位置付けて、実践していくことが必要である。

　○数学への関心・意欲・態度

　○数学的な見方や考え方

　○数学的な表現・処理

　○数量，図形などについての知識・理解

→

→

→

→

本調査では設定なし

「見方や考え方」

「表現・処理」

「知識・理解」

各学年ごとに教科全体の正答率について到達基準との比較を示す。

中３数学は、過去の全国調査の問題を利用しているため、凡例が異なる。

評価の観点別正答率

中学２年生

図１　H23年度（中学２年生数学）評価の観点別正答率

「知識・理解」については、絶対値に関わる内容とグラフ上の点を座標に表すことにおいて、課題が見られた。「表現・処理」については、「図形」と「資料の活用」領域の「表現・処理」に関する問題の正答率が低く、求め方や用語の意味を理解していないことなど、「知識・理解」の定着が十分でないことに要因があるものと考えられる。「見方や考え方」については、「与えられた情報を読み取り、数学的に処理すること」や「問題解決の過程や資料の傾向を説明すること」に課題が見られた。

内容・領域別正答率

中学２年生

「数と式」については、「おおむね達成」の基準を上回ったが、指数の計算、絶対値、方程式の立式などに関わる内容において、課題が見られた。「図形」については、平行・対称・回転移動に関する内容と、扇形の弧の長さや立体の表面積及び回転体の体積の求め方に関する内容において課題が見られた。「関数」については、比例の関係をグラフを表すことは「おおむね達成」の基準を上回ったが、逆にグラフ上の点を座標に表すことや、与えられたグラフを読み取ること、更に読み取ったことを基に数学的に処理したり、問題解決の過程を説明したりすることにおいて、課題が見られた。「資料の活用」については、出題された５問中の４問において、「おおむね達成」の基準を下回る結果となった。設問ごとに見ると、[表現・処理」や「見方や考え方」の問題の正答率が低い結果となっているが、相対度数や有効数字、中央値等の用語の意味や求め方、表し方といった「知識・理解」の定着が十分でないことが、要因であると考えられる。

平成23年度の中学２年生と平成22年度の中学２年生で同一学年の経年比較をすることにより分析を行った。比較の視点については、まず「知識・技能の習得が図れているか」と「知識・技能を活用するための思考力・判断力・表現力が育まれているか」という２点について、基礎的・基本的問題と「活用」に関する問題の結果を基に、分析を行った。また、平成22年度の課題であった「学習指導要領の移行に伴い追加された学習内容が定着しているか」という点についても、関連する問題の結果を基に、分析を行った。

「基礎的・基本的問題」の経年比較（同一学年）
中学２年生

図３　H22・H23年度（中学２年生数学）「基礎的・基本的問題」の正答率の経年比較

「基礎的・基本的問題」については、平成22年度の結果と比べると、正答率は下回った（図３）。設問別に見ると、比例式を解くことや「資料の活用」領域の学習内容などの学習指導要領の移行により追加された学習内容に加え、扇形の弧の長さを求めることについて、知識・技能の定着に課題が見られた。また、絶対値や座標に関わる問題においても、正答率が低かった。要因として、知識が十分定着できていなかったことに加え、文章の意味を十分読み取ることができなかったことが考えられる。
また、表１は、「数と式」の領域の「基礎的・基本的問題」（正の数・負の数や文字の式、方程式等、主に計算の技能を必要とする問題）における各年度ごとの正答率を表したものであり、出題ねらいや「おおむね達成」の基準及び「十分達成」の基準も同じであったため、比較を行った。

表１　H22・23年度（中学２年生数学）「計算の技能を必要とする問題」の正答率の経年比較

５問の平均正答率を比べると、2.8ポイント下回る結果となった。特に、平成23年度は指数を含む計算において課題が見られた。

「活用」に関する問題の経年比較（同一学年）

中学２年生

図４　H22・H23年度（中学２年生数学）「活用」に関する問題の正答率の経年比較

「活用」に関する問題については、平成22年度の結果と比べると、正答率は下回った（図４）。ただ、平成22年度と平成23年度では、出題数が違っていたため、各年度に共通して出題された問題について比較し分析を行った。表２は、与えられた条件をもとにある事柄について説明するような記述式の問題について比較したものであり、表３は数量の関係を見いだし、方程式を作る問題について、比較したものである。

表２　H22・H23年度（中学２年生数学）記述式問題の正答率・無解答率の経年比較

.表３　H22・H23年度（中学２年生数学）数量の関係を見いだし方程式を作る問題の

正答率・無解答率の経年比較

表２と表３から、与えられた条件をもとにある事柄について説明するような記述式の問題と、数量の関係を見いだし、方程式を作る問題においては、平成22年度と同様に、全体の正答率が「おおむね達成」の基準を下回り、課題を残した。

「学習指導要領の移行に伴い追加された学習内容に関する問題」の経年比較（同一学年）
中学２年生

表４　H22・H23年度（中学２年生数学）学習指導要領の移行に伴い追加された

学習内容に関する問題の正答率の経年比較

平成23年度は９問の出題であり、全体の平均正答率は31.8、無解答率は21.6と課題を残す結果となった。平成22年度と比べて正答率の低下や無解答率の増加が見られるのは、記述式及び短答式の問題の割合が増えたこともあるが、全体的に学習指導要領の移行に伴い追加された学習内容においては、基礎的・基本的知識・技能が十分定着できてないことに課題があると考えられる。また、「球の体積の求め方」、「相対度数の求め方」、「有効数字の表し方」については、特に課題があると考えられる。

中学２年生に関しては、上記の「ア結果の概要」と「イ経年比較」から、学習指導要領の移行に伴い追加された学習内容など、特定の「知識・技能」に関する学習内容と、「活用」に関する学習内容において、課題が多いことが確認できた。この２点を踏まえて、正答率が「おおむね達成」の基準を下回った問題を取り上げ、設問ごとに分析を行うことで、より詳細に課題を把握し、具体的な改善点や方策を提示することとした。また、中学校３年生に関しては、過去の全国学力学習状況調査の問題を取り扱ってあるという点を考え、当時の全国平均と比べて正答率の低かった問題を取り上げて分析を行なった。出題された27問中の８問が当時の全国平均を下回り、その内５問が「図形」領域に関わる内容であった。分析の結果から、図形の証明に関わる推論についての理解や論理的な思考力に課題があると考えられる。

学習指導要領の移行伴い追加された学習内容等、特定の学習内容における「知識・技能」の定着に課題がある。

[中学２年生　大問１の（２）]　　
○　問題の概要

○　解答状況

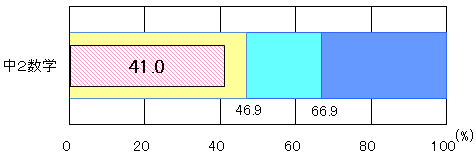
「おおむね達成」の期待正答率50.0に対して、正答率は34.4であり、15.6ポイント下回った。指数の意味や、負の数における指数を含んだ計算方法の理解に課題があると思われる。
○　指導法改善の手立て

生徒がつまずきやすい問題である。指数の意味や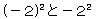等の違いについて理解できるよう丁寧に指導し、類似問題に数多く取り組ませるなど、知識・技能の定着を図る取組が大切である。

[中学２年生　大問２の（１）]　　
○　問題の概要

○　解答状況

「おおむね達成」の期待正答率50.0に対して、正答率は28.3であり、21.7ポイント下回った。分数を絡めた問題であったため、正答率も低下したと考えられる。絶対値や整数の意味や分数についての数値としての大きさの理解に、課題があると考えられる。
○　指導法改善の手立て

絶対値や整数及び自然数等の用語の意味について知識の定着を図る必要がある。また、場合によっては、小学校で学習する小数や分数についての復習が必要である。数の大小を考える場合は、数直線上に表して考えることが多いが、数直線上の目盛りを細かく取るなどの工夫により、該当する数がどの位置にあるのかを理解させて、数値としての大きさを捉えさせていくことが大切である。

[中学２年生　大問２の（４）]　　
○　問題の概要

○　解答状況

学習指導要領の移行に伴い追加された学習内容である。「おおむね達成」の期待正答率50.0に対し、正答率は44.8であり、5.2ポイント下回った。比例式の性質（外項の積＝内項の積）を使った解き方が十分定着できてないものと考えられる。
○　指導法改善の手立て

解が整数であるような場合には暗算でも解は導きやすいが、本問題のように解が分数になるものや、複雑な文字式が絡むような問題においては、比例式の性質（外項の積＝内項の積）を使った解き方が有効である。そのため、比例式の性質を使った解き方についても、十分定着を図ることが大切である。指導に当たっては、２：３＝６：９の場合は、２×９＝３×６が成り立つことなど、具体的で分かりやすい例を取り上げながらまずは知識・理解の定着を図り、その上で、一般的な比例式の問題の解き方へと技能の定着を図っていくことなどが考えられる。

[中学２年生　大問６の（２）]　　
○　問題の概要

○　解答状況

学習指導要領の移行に伴い追加された学習内容である。「おおむね達成」の期待正答率40.0に対して、正答率は18.9であり、21.1ポイント下回った。平行移動、対称移動及び回転移動の理解に課題があると思われる。また、与えられた情報や文章の意味を読み取る力や数学的な思考力を必要としたために、正答率も低下したものと考えられる。

○　指導法改善の手立て

定規やコンパス、分度器等を使いながら、三角形などの具体的な図形を、それぞれの移動を使って移すような操作活動に取り組ませて、知識・技能の定着を図っていくことが、まずは大切であると考える。また、線対称と点対称について学習を終えていることを配慮し、対称移動については線対称としての概念をもたせることや、点対称移動は180°の回転移動であることを理解させることも大切である。更に、本問題のように、ある図形といくつかの移動を使って動かした図形を比べて考えさせる場合においては、厚紙等で作った図形を用いて実際に移動させるなどの操作活動を取り入れることにより、数学的な思考力も培われるとともに知識・技能の定着につながるものと考える。

[中学２年生　大問７の（１）（２）（３）]　　
○　問題の概要

○　解答状況

「おおむね達成」の期待正答率は、問７（1）が50.0、問７（2）が45.0、問７（3）が35.0であったが、正答率は問７（1）が31.7、問７（2）が41.3、問７（3）が8.9と、全てにおいて下回った。与えられた図形や立体の条件に応じて、長さを求めたり、面積を求めたり、体積を求めたりするための知識・技能の定着及び回転体についての理解に課題があると考えられる。また、問７（3）については、球の体積と円柱の体積及び回転体に関する内容が関連した複合問題となっていたため、正答率の低下につながったと考えられる。
○　指導法改善の手立て

図形や立体における長さや面積、体積を求めること等の学習については、十分な時間の確保が大切である。それぞれを学習する過程において、実際に図形や立体の具体物を用いて、長さを測ったり面積を求めたり、体積を調べたりするような操作活動を取り入れていくことで、理解も深まっていくものと考える。そういった学習過程を経た上で、公式を使った求め方を定着させて、技能の習熟を図っていくことが必要である。また、回転体の学習においては、実際に厚紙で作った図形を回転させるなどの操作活動や、パソコンによるグラフィックソフト等を活用した取組を行うことにより、理解が深められるものと考える。

[中学２年生　大問８の（２）]　　
○　問題の概要

○　解答状況

「おおむね達成」の期待正答率55.0に対して、正答率は28.7であり、26.3ポイント下回った。無解答率も21.8であり、座標の意味や表し方についての理解が十分でなかったこと、また、文章の意味を十分読み取ることができなかったことが要因として考えられる。
○　指導法改善の手立て
座標ということばについて理解していても、実際のグラフ上の点や表で表されているxとyの数値と結びついていないことが考えられる。座標、x座標、y座標などのことばの意味を理解させるとともに、y＝－２xなどのグラフの学習において、xに具体的な数を代入しながら表を作る際に、表に表したxとyの値が、それぞれの点の座標やx座標、y座標を表しているということを、実感させるような取組が大切である。また、本問題は複数の解答が考えられたために、戸惑いを感じた生徒も多かったことが予想される。知識・技能に関する内容の学習においても、解答の条件を広く設定した問題に触れさせることは、多様な見方や考え方を育むことにつながっていくものと考える。

[中学２年生　大問９の（１）（２）]　　
○　問題の概要

○　解答状況

問９（1）は「おおむね達成」の期待正答率45.0に対し正答率は21.4で、無解答率は27.4、問９（2）は「おおむね達成」の期待正答率40.0に対し正答率は14.2で、無解答率は34.0であった。与えられたグラフからxとyの関係を読み取って式に表すことや、与えられたグラフの変化や対応の特徴を捉えること、文章の意味を読み取ることなどに課題があると考えられる。
○　指導法改善の手立て

比例の学習内容に関わる発展・応用問題である。問９（1）については、x軸とｙ軸における１目盛り数値が違っていたことも正答率の低下につながったと考えられるが、このような問題を通して、グラフからxとyの関係を読み取り式に表すことできるような技能の習熟を図っていくことが大切である。問９（2）については、Ａの式がｙ＝4/5ｘ、Ｂの式がｙ＝3/10xとなることから4/5x－3/10x＝60という方程式を利用する求め方の他に、50ｇのおもりをつるしたときのばねののびた長さが40－15＝25（mm）になることから、x ： 50＝25 ： 60 など比例式を利用した求め方等も考えられる。このように多様な考え方ができるような課題を設定し取り組ませることで、数学的な思考力の向上につながるものと考える。また、これまで学習したことを活用させることで、知識・技能の定着にもつながるものと考える。

[中学２年生　大問10の（２）（３）、大問11の（１）]　　
○　問題の概要

○　解答状況

学習指導要領の移行に伴い追加された学習内容であり、「おおむね達成」の期待正答率は問10（2）は50.0、問10（3）は50.0、問11（1）45.0であったが、正答率は問10（2）は20.1、問10（3）は42.1、問11（1）は3.7と、全て下回った。相対度数の意味と求め方、度数分布表を利用した平均値の求め方、有効数字の意味と表し方など、知識の定着が十分でないことに要因があると考えられる。
○　指導法改善の手立て

それぞれにおいて、知識の定着を図るための取組が優先事項であると考える。できれば、日常生活の中にある数値で表された情報などを題材とすることで、生徒の関心・意欲を引き出しながら、理解が深められるように授業を進めたい。

多様な見方を用いて考えたり、問題解決の方法や資料の傾向などを説明したりする力に課題がある。

[中学２年生　大問４の（２）]　　
○　問題の概要

○　解答状況

「おおむね達成」の期待正答率35.0に対して、正答率は3.7であり、31.3ポイント下回った。与えられた情報から、条件に合わせて数量の関係を見いだし、方程式に表すという数学的な思考力に課題がある。
○　指導法改善の手立て

本問題は、２つの未知数が問われており、未知数ｘの捉え方によって２通りの方程式が考えられるものであった。太郎さんの考え（お父さんがひろしさんに追いつくまでの時間をxとおいて、２人が進んだ道のりに目を付ける）が一般的であるが、花子さんの考え（お父さんが進んだ道のりをxとおいて、２人が進んだ時間に目を付ける）も理解できるような柔軟な思考力を身に付けさせたいものである。授業においても、本問題のように複数の考え方ができるような問題等を題材として取り扱うことにより、数学的な思考力を培うこともできると考える。

○　解答状況

「おおむね達成」の期待正答率40.0に対して、正答率は19.7であり、20.3ポイント下回った。さらに、無解答率も39.4であった。思考の過程や判断の根拠などを数学的に説明することに課題があると考えられる。
○　指導法改善の手立て

本問題においては、ばねＢのグラフなどの情報をもとに、ばねＢののびた長さが20mmより長くなるおもりの重さ（70ｇ）を捉えて、その根拠について数学的に説明する力が求められている。グラフや式、表に表すという知識・技能の定着を図ることはもちろん大切であるが、それらを「活用」させるような課題の設定や取組も大切である。また、各教科において言語能力の育成が重視されているが、今後の数学の授業においては、解答を求めるだけでなく、思考の過程や判断の根拠などを数学的に説明するような表現力を育むための取組が重要であると考える。

○　解答状況

学習指導要領の移行に伴い追加された学習内容であり、「おおむね達成」の期待正答率35.0に対して、正答率は9.7で25.3ポイント下回り、無解答率は50.4であった。中央値という用語の意味についての知識・理解と資料の傾向を捉えて説明する力に大きな課題があると思われる。
○　指導法改善の手立て

推論についての理解や論理的な思考力に課題がある。

[中学３年生　大問６]　　
○　問題の概要

○　解答状況

実施時の全国の正答率28.9に対して、正答率は26.1であり、2.8ポイント下回った。証明の意義についての理解に課題があると考えられる。
○　指導法改善の手立て

帰納的な方法は、図形の性質や関係性を見いだす方法としては有効であるが、その一般性を保証するものではない。このように帰納的な方法の意義と限界を理解させ、演繹的な推論による証明により、命題が例外なしに成り立つことを明らかにできることについて理解を深めさせることが大切である。本問題を授業で扱う場合には、いくつかの三角形について内角の和が180°であることを調べるという帰納的な方法により、その事柄の信頼性を高めることはできるが、全ての三角形についてその事柄が正しいかどうかを調べることができないことを確認する必要がある。その上で、全ての三角形に対応できる文字を用いて演繹的に説明する証明が必要であることを理解できるようにすることが大切である。

[中学３年生　大問１２]　　
○　問題の概要

○　解答状況

問12（2）は記述問題であったため、問12（1）、問12（3）と比べると正答率も低く、無解答率は高い状況にある。しかしながら、問12（1）と問12（3）については、実施時の全国の正答率と比べて、正答率がそれぞれ4.1ポイント、1.3ポイントと下回ったが、問12（2）については、実施時の全国の正答率を8.6ポイントと上回った。このことから、証明の進め方等の技能については習熟が図られているが、証明の方針を立てるときの根拠や、証明した事柄から新たに分かることの理解において、課題があると考えられる。
○　指導法改善の手立て

方針を立て証明を書くことができるようにすることは大切であるが、加えて、証明の中で使われている根拠を正確に表現したり、証明された事柄から新たな性質等を見いだしたりできるようにすることが大切である。指導に当たっては、本問題のような証明問題を取り扱う場合に、「合同だから」と使っている根拠を、「合同な図形の対応する辺の長さは等しいから」と正確に表現させることによって、証明が分かりやすくなることを実感する機会を作ることが考えられる。また、ある事柄についての証明ができた段階において、証明された事柄以外で成り立つことを問うことにより、新たな性質や関係を見いだすように促すことが考えられる。

今回の調査によって明らかになった指導改善のための重点項目は、次の通りである。
(ア)  基礎的・基本的な知識・技能の定着を図ること。特に、学習指導要領の移行により追加された学習内容等、課題が見られる学習内容における知識・技能の定着を図ること。
(イ)  身に付けた知識・技能を基に、それらを活用したり、数学的な表現を用いて問題解決したりすることができるような数学的な思考力・判断力・表現力を育むこと。
以上の２つの重点項目を踏まえて、学習指導の改善を図っていく必要がある。数学的活動についても、２つの重点項目を踏まえて、実施していくことが大切である。具体的に言うと、数学的活動を日々の授業の中にどのように位置付け、また、どのような活動に取り組ませた方が効果的であるかということを常に考えながら、授業の改善を図っていくことが大切である。
※数学的活動は、基礎的・基本的な知識・技能を確実に身に付けるとともに、数学的に考える力を高めたり、数学を学ぶことの楽しさや意義を実感させたりするために、重要な役割を果たすものである。　

(ア)  基礎的・基本的な知識・技能の確実な定着に向けて
「球の体積の求め方」や「相対度数の求め方」、「有効数字の表し方」などの学習指導要領の移行により追加された学習内容に加え、「扇形の弧の長さ求めること」や「グラフから式を読み取ること」等、特定の学習内容における知識・技能の定着に課題があることが分かった。数学的な思考力や表現力の向上を目的とした数学的活動を取り入れた授業実践を重視することはもちろん大切であるが、こればかりを重視し過ぎれば、逆に思考力や表現力を育むための基盤となる基礎的・基本的な知識・技能が定着が図れないといった悪影響も考えられる。数学的活動の役割にもあるように、３つの点（「知識・技能を確実に身に付ける」、「思考力・判断力・表現力を高める」、「数学を学ぶことの楽しさや意義を実感させる」）のバランスと連動性を考えながら、授業改善を図ることが大切である。また、１学年の「資料の活用」領域の学習内容については、他の領域の学習内容との関連性が薄いため、その分他の領域に比べて知識・技能が定着できてないことが現実的に考えられる。知識・技能の定着に向けての取組として、単元指導計画の見直しをしたり、定期的に小テストを行ったり、補充的な学習を行ったりすることが必要である。

（イ）  数学的な思考力・判断力・表現力の向上を目指して　

数学的な思考力・判断力・表現力を育むためには、それらを意図した数学的活動を取り入れた授業実践を積み重ねていくことが必要である。ただ、(ア)にも述べたように、授業実践をする上において、基礎的・基本的な知識・技能の定着を図る視点も忘れてはならない。 その上で、「概念・法則などを解釈し、説明したり活用したりする活動」、「与えられた情報を分析・評価したり論述したりする活動」、「互いの考えを伝え合い、自らの考えや集団の考えを発展させる活動」など、言語活動を重視した数学的活動の充実を図っていくことが大切である。また、通常の授業で取り扱う題材や課題は、その領域だけの内容を中心としたものが多いため、生徒の学習意欲を引き出すことができなかったり、生徒が各領域の学習内容を関連性のないものと捉えたりすることが考えられる。そこで、身近な実生活に結びつきのあるものや多様な考え方ができるものなど、題材や課題についての設定の工夫を行っていくことが大切である。さらに、機会を捉えて、各領域の学習を相互に関連付けたストーリー性のある授業を意図的に設定したり、関連する学習プリントに取り組ませたりすることで、生徒の多様な考え方や柔軟な発想を引き出すことにつながり、数学的な思考力・判断力・表現力が育まれていくものと考える。