|
|
単元「図形の調べ方」の小単元「多角形の角」(4時間)における数学的活動を取り入れた授業モデルです。
下の授業展開案を授業にご活用ください。 |
| |
単元 図形の調べ方 (啓林館) |
1 平行と合同 |
【・2・ 多角形の角】 全4時間 |
| |
| |
ねらい |
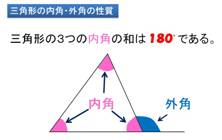
・ 三角形の3つの角の和が180°であることを平行線と角の性質を使って確かめようとす
る。
・ 三角形の3つの角の和が180°になることを帰納的に考察することができる。 |
段階 |
|
つかむ |
| ○教科書88ページの「ふりかえり」を基に、三角形の3つの角の和が180°であることを思い出す。 |
| ○本時の学習内容「三角形の3つの内角の和が180°であることを、平行線と角の性質を使って確かめよう」を知る。 |
|
|
見通す |
| ●三角形の紙を切り分け、3つの角を集めると、一直線になることに気付く。 |
|
練り合う |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●補助線をひき、「平行線と錯角」「平行線と同位角」の関係や「一直線の角は180°である」ことを使って、説明する。 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
|
深める |
| ●教科書88ページ「自分のことばで伝えよう」を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●グループのメンバーで互いに、自分の考えを説明し合う。 |
|
まとめる |
|
|
|
|
ねらい |
・ 図形の用語を理解する。
・ 三角形の内角・外角の性質を理解する。
・ 三角形の内角・外角の性質を利用して角の大きさを求めることができる。 |
段階 |
|
つかむ |
| ○本時の学習内容「図形の用語について学ぼう」を知る。 |
|
|
見通す |
| ○三角形の外角と内角を定義する。 |
| ○前時の学習内容を、内角、外角の用語を使ってまとめる。 |
| ○鋭角、鈍角を知り、三角形を内角の大きさに目を付けて分類する。 |
|
練り合う |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
|
深める |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
|
まとめる |
|
|
|
|
|
・ 多角形の内角の和を求めようとする。
・ 多角形の内角の和を予想し、それが正しいことを既習のことに帰着させて考える
ことができる。 |
段階 |
|
つかむ |
|
|
見通す |
●課題1を考える。
|
| ○発表を基に、六角形の内角の和の求め方について確認する。 |
|
練り合う |
○課題2を考える。
| n角形の内角の和は、どのような式で表せるのだろう。 |
|
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
| ○n角形の内角の和が、180°×(n−2)であることを確認する。 |
| 数学的活動 〔目の前の課題から、物事の本質を見抜こうとする活動〕 |
| ●n角形の内角の和を求めるために必要な条件を考える。 |
|
深める |
●課題3を考える。
n角形の内部に点Pをとり、下の図のように三角形に分けました。
下の図を利用して、次の問いに答えなさい。
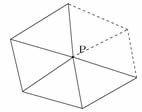
(1) このときのn角形の内角の和を求める式を,次のア〜ウの中から1つ選びなさい。
ア 180°×n−360°
イ 180°×(n−2)
ウ 180°×(n−1)−180°
(2) (1)で選んだ式になる理由を説明しなさい。 |
|
|
まとめる |
| ●課題3を基に、n角形の内角の和を求めるために必要な条件を振り返る。 |
| ●180°×(n−2)の考えと、180°×n−360°の考えは、どちらでも多角形の内角の和を求めることができることを確認する。 |
|
|
|
〈実践を終えて〉
◇ 数学的活動について
・「成り立つ事柄を予想する活動」として、課題1の結果について予想させました。その際、全員が取り組むことができるように、3つの選択肢から選ぶという方法を取り入れました。その結果、1人1人が自分の考えをもって、次の六角形の内角の和を求めるという活動に進むことができました。
・六角形の内角の和を求める場面では、「成り立つ事柄を予想する活動」や「観察、操作などの具体的な活動」を取り入れたことで、ほとんどの生徒が、既習事項の三角形の性質と関連付けて解決することができました。さらに、そこで出された多様な見方を基に、n角形の内角の和の求め方について一般化していくことができました。 |
◆ 学習評価について
・数学への関心・意欲・態度の観点については、課題2を考える活動(詳細授業展開案の学習活動の5)で評価を行い、n角形の内角の和を求める式をつくる課題への取組の状況を見取りました。個人で考えた後、グループ活動を取り入れました。その結果、互いの考えを出し合いながら、課題の解決を図ったため、ほとんどの生徒が「おおむね満足できる状況」(B)に達することができました。
・数学的な見方や考え方の観点については、課題3を考える活動(詳細授業展開案の学習活動の7)でのワークシートの記述で評価を行いました。授業の最後にワークシートを回収して個別に評価を行い、単元における総括の資料としました。また、「おおむね満足できる状況」(B)に達していない生徒には、返却時に補助プリントを用いて支援を行いました。
|
|
◆ ICT利活用について
・既習事項を復習する場面や課題2の求め方を確認する場面で、電子黒板を用いて説明を行いました。図形領域では板書に時間が掛かるため、振り返らせたい既習事項やn角形の求め方をパワーポイントで提示しました。このようにしたことで、説明の時間を短縮することができ、個人やグループでの活動の時間を十分確保することができました。
・発表をさせる場面では、書画カメラで生徒の記述を提示しながら説明させたため、図、式、言葉などを関連付けて考えさせることができ、理解が深まりました。 |
|
|
ねらい |
・ 多角形の外角の和を求めようとする。
・ 多角形の外角の和を演繹的に考察することができる。
・ 多角形の外角の和を利用し、様々な多角形の外角の大きさを求めることができる。 |
段階 |
|
つかむ |
| ○小テストとして、前時の内容を復習する。 |
| ○本時の学習内容「多角形の外角の和について考えてみよう」を知る。 |
|
|
見通す |
| ●三角形と四角形の外角の和では、どちらの和が大きいかを予想する。 |
|
練り合う |
| ●三角形の外角、四角形の外角を実測して、その和の大きさを比べる。 |
| ●五角形の外角の和やn角形の外角の和について、予想する。 |
| ○三角形の場合を参考にして、同じようなやり方で、四角形や五角形の外角の和を計算で求める。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
| 数学的活動 〔目の前の課題から、物事の本質を見抜こうとする活動〕 |
●n角形の内角の和 180°×n−360°を使って、外角の和を導く。
|
| ○多角形の外角の和は360°であることを確認する。 |
|
深める |
| ○教科書92ページの問5、93ページの問6を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分で考察したことをグループの中で説明し、他の意見を書き加える。 |
| ○グループで話し合ったことを基に、全体に伝える。 |
|
まとめる |
| ●多角形の外角の和は360°であることを振り返る。 |
|
|
|
|