過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
[問題1]
ある町には図のような道があります。アユミさんは遠回りをせずにカオリさんのいるところへ行こうと思います。
その道順は全部で何とおりありますか。
|
|
| ○ |
問題を提示する際には、図を示しながら説明することで、題意をとらえやすくする。 |
|
|
|
| |
・ |
アユミさんのいるところからカオリさんのいるところへ行く道は何とおりあるか調べる方法を考える。 |
 |
「ノートを見ながら通り方を考えている様子」 |
| |
≪予想される児童の反応≫ |
| |
・ |
「道に記号や名前をつけてみたら行き方が分かりやすいかな。」 |
| |
・ |
「交差点に記号や名前をつけてみたらどうかな。」 |
| |
・ |
「右、左、上、下と書いてみたら。」 |
| |
・ |
「行き方を色分けしてみたらどうかな。」 |
| |
≪児童が実際にかいた考え≫ |
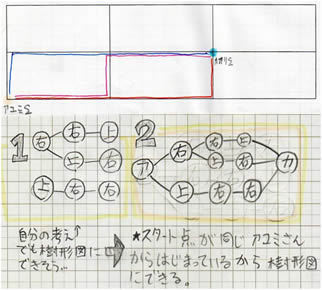 |
[問題2]
アユミさんは遠回りをせずにサユリさんのいるところへ行こうと思います。
その道順は全部で何とおりありますか。
|
|
| ○ |
児童にとって、問題文にある「遠回りをしない」という条件や道順を図(樹形図)や表にして表記することが難しいので、解決が簡単な[問題1]を例題として取り組ませる。 |
| ○ |
教師が黒板の図を用いて、「遠回りをしない」という条件を確認して、何通りあるかを考えさせる。
|
| ○ |
前時までの学習を振り返らせることで、図(樹形図)や表を使って道順を考えることができないか考えさせる。 |
| ○ |
道や交差点は記号化すると簡単だということに気付かせる。 |
| ○ |
[問題1]では、道順が3通りあることを確認する。 |
|
見通す |
2 |
解決の見通しをもつ。 |
| |
・ |
アユミさんのいるところからサユリさんのところへ行く道は何通りあるか調べる方法を考える。 |
|
| ○ |
[問題1]と[問題2]のサユリさんのいる場所の違いを確認し、道順が全部で何通りになるのか予想させる。 |
| ○ |
[問題1]で考えた解決方法が同じように使えないのか考えさせる。 |
|
| 自力解決 |
3 |
自力解決をする。 |
| |
・ |
道順を図(樹形図)や表にして、自分の考えをかく。(ア) |
|
| ◎ |
友達に分かりやすく説明できるように、ノートに言葉などを入れさせる。(ア) |
|
| 学び合い |
4 |
自分の考えをペアで説明し合う。 |
| |
・ |
ノートを見せながら、自分の考えを説明する。(イ) |
 |
「ノートを見せながら説明している様子」 |
|
| ◎ |
道順を、図(樹形図)や表を示させながら、相手意識をもたせて説明させる。(イ) |
| ○ |
自分のやり方と同じか違うかを意識させながら聞かせる。また、よく分からないところは、お互いに質問し合うように促す。 |
| |
|
| |
|
| |
|
|
5 |
解決方法を発表し、全体で話し合う。
|
| |
・ |
全体の場で説明する。(イ) |
 |
「実物投影機に映したノートと黒板の図を使い
2人で説明している様子」 |
| |
≪児童が実際にノートにかいた考え≫ |
| |
|
| ◎ |
実物投影機を使って児童のノートをスクリーンに映し、説明させる。(イ) |
| ○ |
図(樹形図)を用いて表すことで、道順を落ちや重なりがなく順序よく整理できることを理解させる。 |
| ○ |
道順は6通りになることを、全体の場で確認する。 |
◇起こり得る場合を順序よく整理し、条件に合う道順を考えている。
【数学的な考え方】[ノート、行動観察] |
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
・ 樹形図に表して整理すると分かりやすい。 |
| |
|
|
| 7 |
本時の学習を算数日記にまとめる。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
|
|
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
| ○ |
新しい友達のいる場所の問題を提示し、本単元で学習した解決の方法を活用してみたいという意欲を喚起する。 |
|