| ア |
結果の概要 |
| |
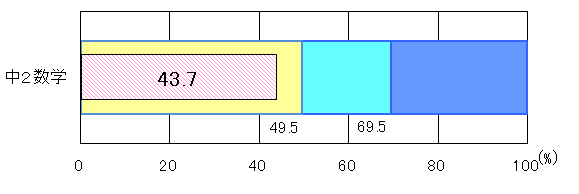
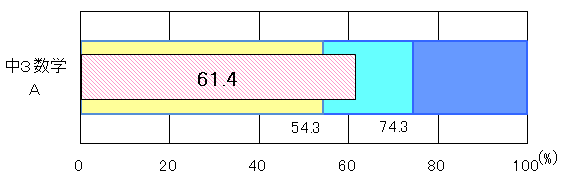
各学年ごとに教科全体の正答率について到達基準との比較を示す。
 |
(ア) |
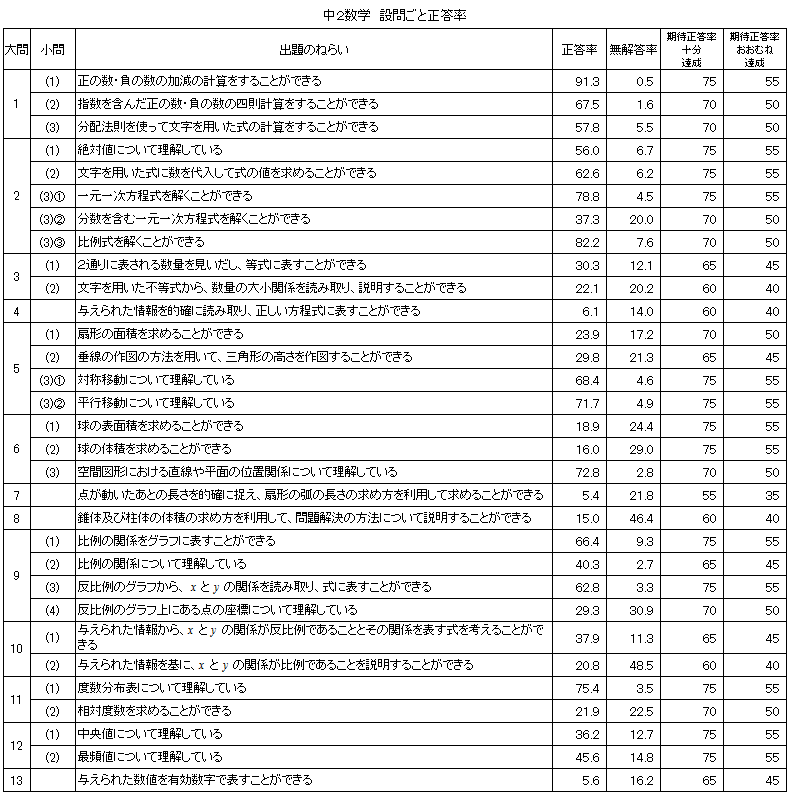
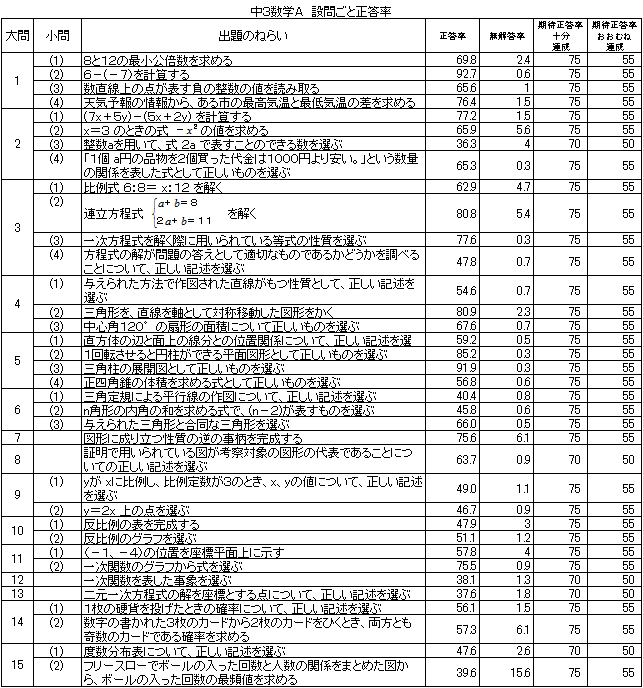
教科及び設問ごと正答率 |
| |
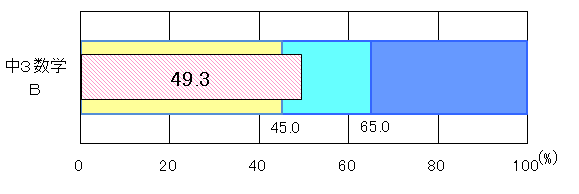
中学2年生において、教科正答率は「おおむね達成」の基準を5.8ポイント下回り、出題された全31問中18問が「おおむね達成」の基準を下回った。中学3年生において、「A問題」の教科正答率は「おおむね達成」の基準を7.1ポイント上回り、出題された36問中23問が「おおむね達成」の基準を上回った。「B問題」の教科正答率は「おおむね達成」基準を4.3ポイント上回り、出題された全15問中10問が「おおむね達成」の基準を上回った。
|
| |
|
(イ) |
評価の観点別正答率
中学2年生
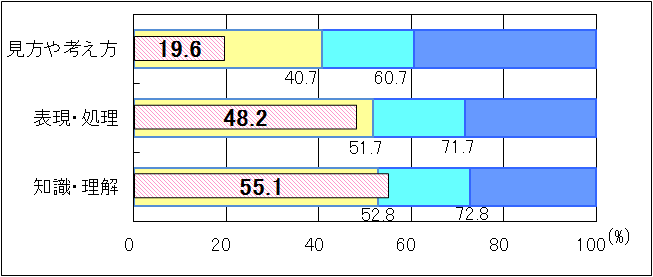 |
図1 H24年度(中学2年生数学)評価の観点別正答率
|
「知識・理解」については、「おおむね達成」の基準を2.3ポイント上回る結果となったが、「中央値、最頻値などの用語に関すること」や「グラフ上の座標に関すること」には課題が見られた。「表現・処理」と「見方や考え方」については「おおむね達成」の基準を下回った。「表現・処理」については、「球や扇形に関すること」や「相対度数や有効数字に関すること」の設問の正答率が低かった。「見方や考え方」については、「与えられた情報を的確に読み取り、正しい方程式に表したり、数学的に処理したりすること」や「与えられた情報を基に、比例であることを説明すること」の設問の無解答率が高かった。
|
| |
中学3年生
①A問題
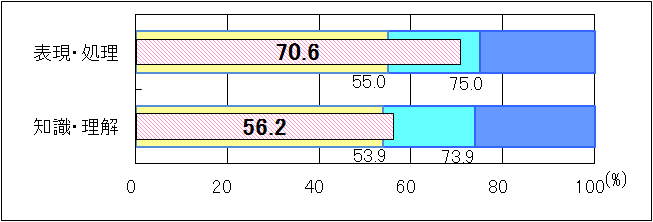 |
図2 H24年度(中学3年生数学「A問題」)評価の観点別正答率
|
「表現・処理」と「知識・理解」については共に「おおむね達成」の基準を上回った。しかしながら、「表現・処理」については、「反比例の関係を表す表を完成すること」には課題が見られた。「知識・理解」については、「文字の値が整数のときに、式の値について考察すること」「二元一次方程式の解とグラフの関係に関すること」「2つの数量関係が一次関数になること」などには課題が見られた。
|
| |
②B問題
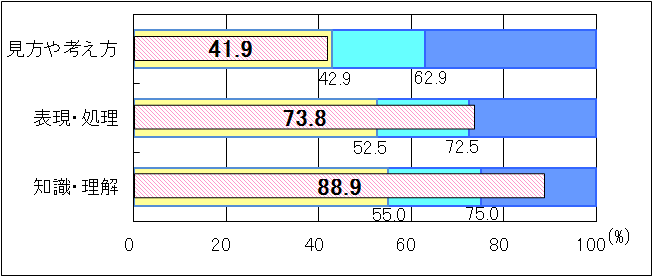 |
図3 H24年度(中学3年生数学「B問題」)評価の観点別正答率
|
「表現・処理」と「知識・理解」については共に「十分達成」の基準を上回ったが、「見方や考え方」については、中学2年生と同様に「おおむね達成」の基準を1.0ポイント下回った。「見方や考え方」については、「事柄が成り立つ理由や問題解決の方法について説明すること」や「数量の関係を数学的に解釈し、数学的な表現を用いて説明すること」などの設問の無解答率が高かった。
|
| |
|
(ウ) |
内容・領域別正答率
中学2年生
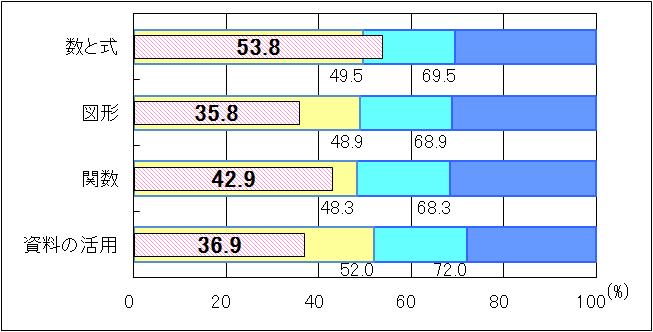 |
図4 H24年度(中学2年生数学)内容・領域別正答率
|
「数と式」については、「おおむね達成」の基準を4.3ポイント上回ったが、「正しい方程式に表すこと」「不等式から、数量の大小関係を読み取り、説明すること」には課題が見られた。「図形」については、「扇形の弧の長さの求め方を利用すること」「球に関すること」などの設問の正答率が低かった。「関数」については、「与えられた情報を基に、比例であることを説明すること」「グラフ上の座標に関すること」「与えられた情報から反比例であることとその関係を式に表すこと」に課題が見られた。「資料の活用」については、「有効数字、中央値、最頻値などの用語に関すること」「相対度数を求めること」などの設問の正答率が低かった。 |
|
中学3年生
①A問題
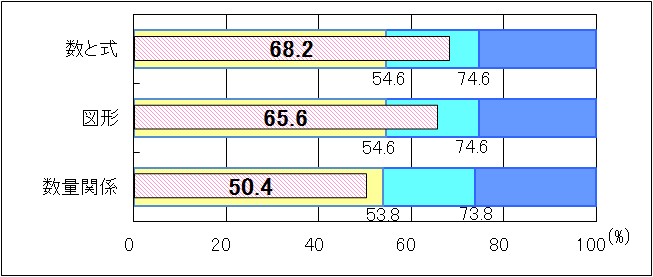 |
図5 H24年度(中学3年生数学「A問題」)内容・領域別正答率
|
「数と式」については、「おおむね達成」の基準を3.6ポイント上回ったが、「文字の値が整数のときの式の値についての考察すること」には課題が見られた。「図形」についても「おおむね達成」の基準を9.0ポイント上回ったが、「平行線の作図に関すること」「内角の公式の意味の理解に関すること」には課題が見られた。「数量関係」については、「比例や反比例の表、式、グラフに関すること」「最頻値や度数分布に関すること」などの設問の正答率が低かった。 |
|
②B問題
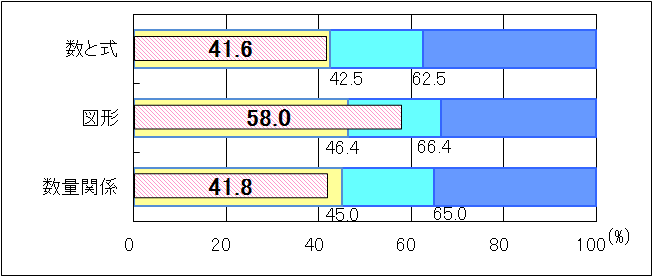 |
図6 H24年度(中学3年生数学「B問題」)内容・領域別正答率
|
「数と式」については、「おおむね達成」の基準を0.9ポイント、「数量関係」については3.2ポイント下回り、「数学的な表現を用いて説明すること」「事柄が成り立つ理由を説明すること」「数量の関係を数学的に解釈すること」などの設問の無解答率が高かった。「図形」については、「おおむね達成」の基準を11.6ポイント上回っていたが、「問題解決の方法を数学的に説明すること」に課題が見られた。 |
| |
|
| |
|
| イ |
|
| |

中学2年生では、平成23年度の課題であり、「おおむね達成」の基準を下回った「基礎的・基本的な問題」と、「活用」する力を問う問題、「移行に伴い追加された学習内容」についての変容を考察するため、同一学年の経年比較を行った。また、中学3年生では、同一出題主旨で達成基準が等しい「A問題」について考察するため、平成23年度の秋に実施された問題と平成24年度の問題を同一学年で経年比較した。「B問題」については、平成23年度に「おおむね達成」の基準を下回ったものが多かった、記述式を中心に変容を考察するため、また、2年間の学習状況の変容を考察するため、同一生徒の1年生の内容である平成23年度2年生の問題と平成24年度3年生の「A問題」「B問題」の中から1年生の内容を抽出した問題を比較し、評価の観点別正答率にまとめ、考察を行った。
|
| |
|
(ア) |
「基礎的・基本的問題」の経年比較(同一学年)
中学2年生
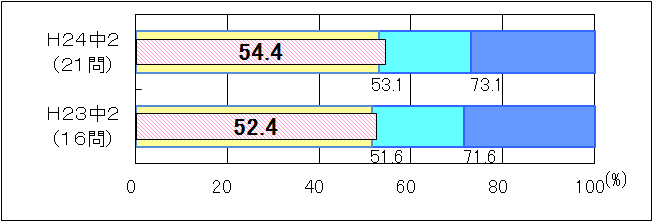 |
図7 H23・H24年度(中学2年生数学)「基礎的・基本的な問題」の正答率の経年比較 |
「基礎的・基本的な問題」については、「おおむね達成」の基準が異なるために、単純に比較することはできないが、平成23年度と比べると、正答率は上回る結果となった(図7)。設問別に見ると、「分数を含む一元一次方程式」「球や扇形に関すること」「反比例のグラフの上の座標に関することや比例に関すること」「数学の用語に関すること」に課題が見られた。
また、表1は「数と式」の領域の「基礎的・基本的な問題」(正の数・負の数や文字の式、比例式等、主に計算の技能を必要とする問題)における年度ごとの正答率を表したものである。出題のねらいや「おおむね達成」の基準及び「十分達成」の基準も等しかったため、比較を行った。
表1 H23・24年度(中学2年生数学)「計算の技能を必要とする問題」の
正答率の経年比較
|
 |
4問の平均正答率を比べると、17.8ポイント上回る結果となり、改善が図られてきているが、「分配法則を用いた文字の計算」については、平成23年度より0.2ポイント下回る結果となった。 |
中学3年生数学A問題
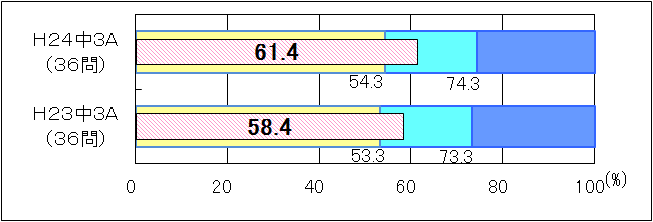 |
図8 H23・H24年度(中学3年生数学A問題)の正答率の経年比較 |
「基礎的・基本的な問題」については、「おおむね達成」の基準や「十分達成」の基準が異なるため単純に比較することはできないが、平成23年度と比べると、正答率は上回る結果となった(図8)。設問別に見ると、中学2年生と同様に「数量関係」の「比例と反比例の表、式、グラフに関すること」に課題が見られた。また、「二元一次方程式の解とグラフに関すること」「作図に関すること」「数学の用語に関すること」など、「知識・理解」に関することの習得に課題が見られた。
また、表2は、「同一の出題の趣旨」における年度ごとの正答率を比較したものであり、「おおむね達成」の基準及び「十分達成」の基準も等しかったため、比較を行った。
表2 H23・24年度(中学3年生数学A問題)「同一の出題の趣旨」の
正答率の経年比較
|
 |
4問の平均正答率を比べると、10.7ポイント上回る結果となり、改善が図られてきているが、「整式の加法と減法の計算」については、平成23年度より5.6ポイント下回る結果となった。 |
| |
|
(イ)
|
「活用」に関する問題の経年比較(同一学年)
中学2年生
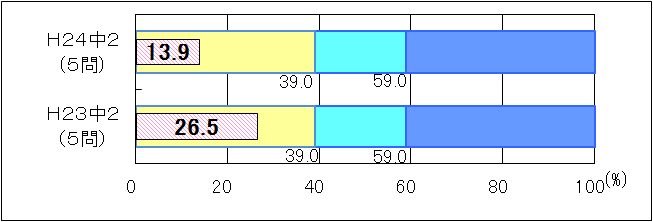 |
図9 H23・H24年度(中学2年生数学)「活用」に関する問題の正答率の経年比較 |
「活用」に関する問題については、「おおむね達成」の基準及び「十分達成」の基準も等しかったため、比較を行った。平成23年度と比べると、正答率が12.6ポイント下がり、課題が見られる結果となった(図9)。表3は、与えられた情報を読み取り、数学的な表現を用いて説明するなどの言葉や数を使って説明する問題について比較したものである。また、表4は、数量の関係を見いだし、方程式をつくる問題について比較したものである。
表3 H23・H24年度(中学2年生数学)記述式問題の
正答率・無解答率の経年比較
|
 |
 |
.
表4 H22・H23・H24年度(中学2年生数学)数量の関係を見いだし方程式をつくる問題の
正答率・無解答率の経年比較 |
|
表3、表4より与えられた情報を読み取り、数学的表現を用いて説明するような記述式の問題と数量関係を見いだし、方程式を作る問題については、平成22年度から継続して、全体の正答率が「おおむね達成」の基準を下回り、課題を残す結果となった。 |
| |
|
|
「活用」に関する問題の経年比較(同一学年)
中学3年生
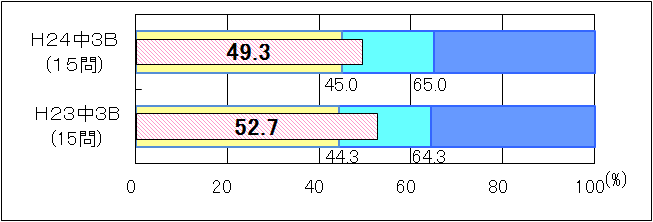 |
図10 H23・H24年度(中学3年生数学B問題)の正答率の経年比較 |
B問題については、「おおむね達成」の基準及び「十分達成」の基準が異なるために単純に比べることができない。しかし、平成23年度より「おおむね達成」の基準が上がっているのにもかかわらず、正答率が下がる結果となった。表5については、数学的な表現を用いて説明したり、問題解決の方法を説明したりするなどの記述式の問題について比較したものである。
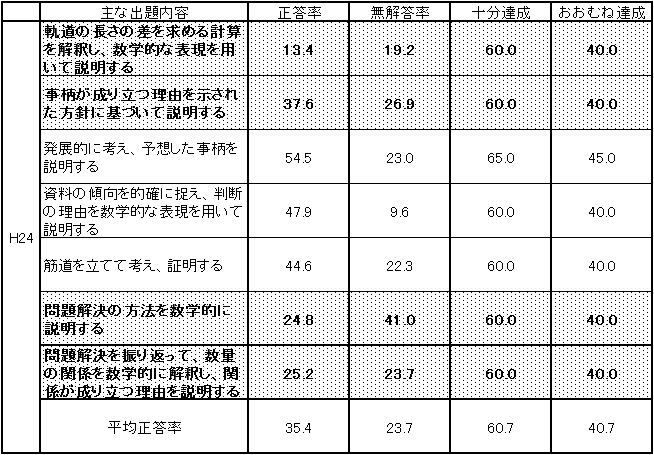
表5 H23・H24年度(中学3年生数学)記述式問題の正答率・無解答率の経年比較
|
 |
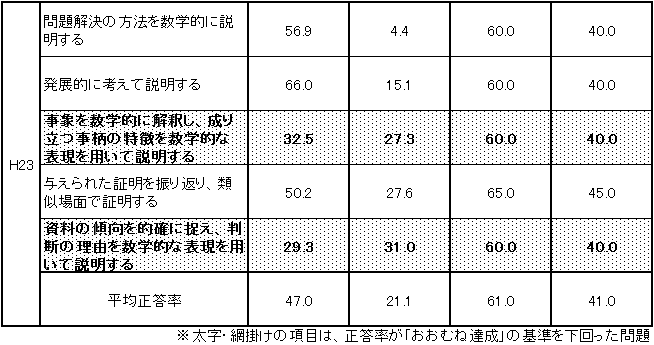 |
.「おおむね達成」の基準と「十分達成」の基準が異なるために単純に比較することはできないが、記述式問題の平均正答率は平成23年度と比較すると、11.6ポイント下がり、無解答率は2.6ポイント上がる結果となった。中学2年生同様に「数学的な表現を用いて説明すること」「理由について説明すること」に関しては平成23年度と引き続き課題を残す結果となった。 |
| |
|
(ウ) |
「学習指導要領の移行に伴い追加された学習内容に関する問題」の経年比較(同一学年)
中学2年生
表6 H23・H24年度(中学2年生数学)学習指導要領の移行に伴い追加された
学習内容に関する問題の正答率の経年比較
|
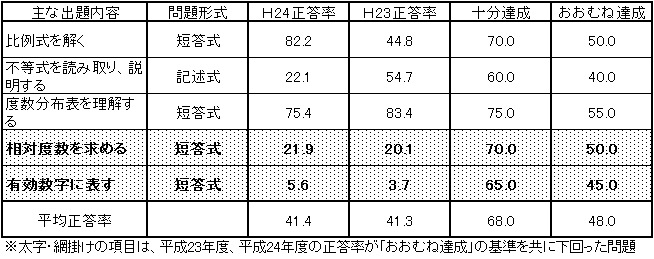 |
表6は、「おおむね達成」及び「十分達成」の基準が等しい問題を取り上げて比較を行った。平均正答率は、平成24年度は41.4、平成23年度は41.3となり、共に「おおむね達成」の基準を下回り、「資料の活用」については、平成23年度に引き続き課題を残す結果となった。 |
| |
|
|
「学習指導要領の移行に伴い追加された学習内容に関する問題」の経年比較(同一学年)
中学3年生
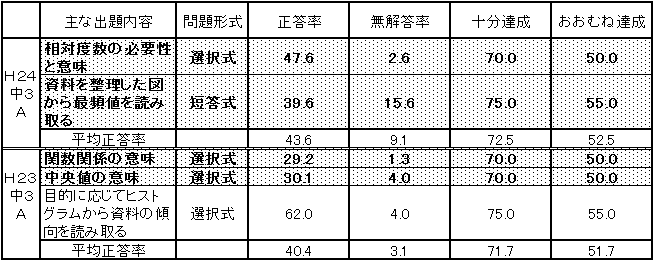
表7 H23・H24年度(中学3年生数学)A問題及びB問題についての学習指導要領の
移行に伴い追加された学習内容に関する問題の正答率の経年比較 |
 |
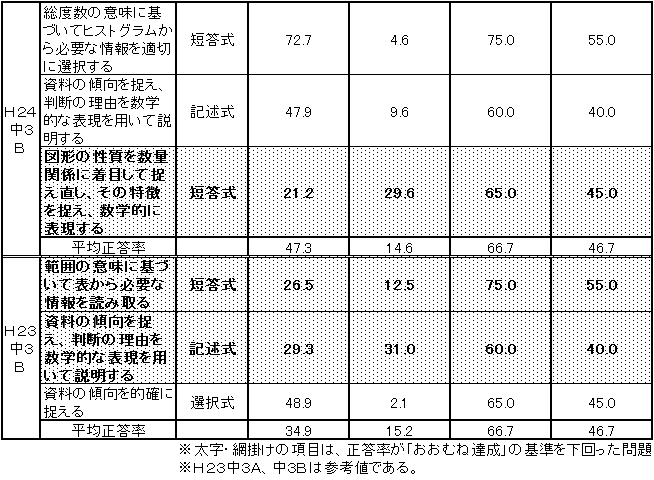 |
表7より学習指導要領の移行に伴い追加された学習内容については、「B問題」については、平成23年度より改善が図られてきているが、「A問題」については、依然として「おおむね達成」の基準に到達することができていない。特に中学2年生と同様に「資料の活用」に課題が見られる結果となった。 |
| |
|
(エ) |
平成23年度2年生及び平成24年度中学3年生(「A問題」「B問題」の1年生出題内容)の経年比較(同一生徒)
|
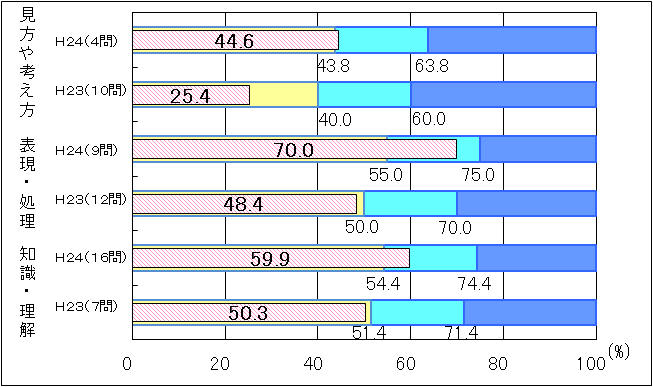
図11 H23年度中学2年生・H24年度中学3年生の観点別正答率の経年比較 |
「おおむね達成」及び「十分達成」の基準が異なるために、単純に比較することはできないが、平成23年度中学2年生は、「おおむね達成」の基準を全ての観点で下回ったが、平成24年度中学3年生は「おおむね達成」の基準を全ての観点で上回った。しかし、平成23年度に引き続き、「知識・理解」では、「比例や反比例の表、式、グラフに関すること」「度数分布表や最頻値の用語に関すること」に課題が見られた。「見方や考え方」では、「数学的な表現を用いて説明すること」に課題が見られる結果となった。 |
| |
|
| |
|
| ウ |
設問ごとに見た傾向と指導改善の手立て |
|
上記の「ア結果の概要」と「イ経年比較」から、学習指導要領の移行に伴い追加された知識・技能に関する学習内容、特定の基礎的・基本的な知識・技能に関する学習内容、数学的な表現を用いて説明するなどの記述式の学習内容に課題が見られた。これらを踏まえて、設問ごとに分析を行うことで、より課題を詳細に把握し、具体的な改善策や方策を提示することとした。 |
| |
|
傾向1 |
学習指導要領の移行に伴い追加された知識・技能に関する学習内容の習得に課題がある。
[中学2年生 大問6]
○ 問題の概要
○ 解答状況
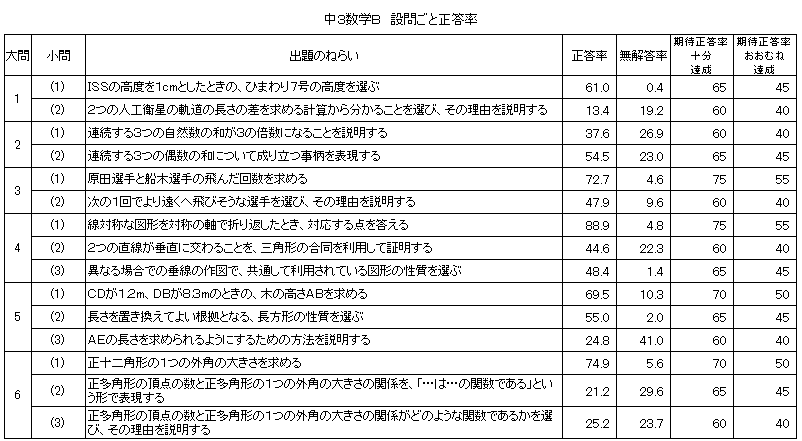
「おおむね達成」の期待正答率55.0に対して、問6(1)の正答率が18.9で36.1ポイント、問6(2)の正答率が16.0で39.0ポイント下回った。与えられた図形や立体において、長さ、面積や体積を求める等の知識・技能の習得に課題があると考えられる。特に、公式を用いて数を当てはめて値を求めることに課題があると考えられる。
○ 指導改善の手立て
球の表面積については、模型を用いたり、実験による測定を行ったりして、実感を伴って理解できるようにすることが必要である。また、底面の半径が等しく、高さが底面の直径になるような円錐、球、円柱の体積を求め、比較させることを通して、体積比が1:2:3になることを確認させることでより理解が深まるような指導を行っていくことが大切である。
[中学2年生 大問11、大問12、大問13〕
○ 問題の概要
○ 解答状況
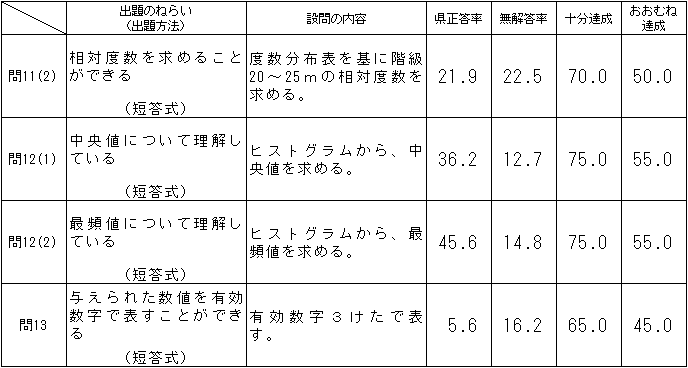
「おおむね達成」の期待正答率は、問11(2)は50.0、問12(1)(2)は55.0、問13は45.0であったが、正答率は、問11(2)は21.9、問12(1)は36.2、問12(2)は45.6、問13は5.6と、全て下回った。相対度数の求め方、中央値、最頻値等の用語に関すこと、有効数字の表し方などの知識の確実な習得に課題があると考えられる。
| [中学3年生「A問題」 大問15〕 |
 |
○ 解答状況
問15(1)の正答率は、「おおむね達成」の期待正答率50.0に対して、47.6で2.4ポイント下回り、問15(2)は、期待正答率55.0に対して、正答率が39.6で15.4ポイント下回った。相対度数の意味や最頻値についての知識の習得に課題があると考えられる。
○ 指導改善の手立て
大きさの異なる2つ以上の資料の傾向を比較するためには、相対度数が必要であることを実感させる必要がある。そのままの階級の度数を比較した場合と相対度数を比較した場合の結果が異なる場面を設定し、より理解を深めさせたいと考える。代表値を用いて資料の傾向を読み取る場合には、平均値、最頻値、中央値等を求め、これらを適切に使用し比較できるようにする場面を設定する必要がある。特に、日常生活の身近な題材を数値として取り上げ、数学を多くの場面で活用できることを実感させながら、資料の傾向を比較させることが大切である。また,資料を整理する際に,コンピュータを利用して代表値や相対度数を求めさせ、資料の傾向を捉え説明することができるような活動を数多く取り入れる必要がある。 |
| |
|
傾向2 |
特定の基礎的・基本的な知識・技能に関する学習内容の習得に課題がある。
[中学2年生 大問4]
○ 問題の概要
○ 解答状況
問4は「おおむね達成」の期待正答率40.0に対して、正答率が6.1で、33.9ポイント下回った。与えられた情報から数量を読み取り、文字を用いた式に表すことに課題があると考えられる。
○ 指導改善の手立て
方程式をつくる際には、問題の中の数量やその関係から2通りに表される数量を見いだし、文字を用いた式や数で表すことができるようにすることが大切である。表、言葉の式や線分図等で表す活動を取り入れ、問題場面の理解を深められるようする。数量を文字を用いて式に表すことができるようにするために、具体的な数を取り上げて式に表したり、文字を用いた式を読み取ったりする活動を取り入れていく必要がある。
[中学2年生 大問5]
○ 問題の概要
○ 解答状況
問5(1)は「おおむね達成」の期待正答率50.0に対して、正答率が23.9で、26.1ポイント下回った。扇形の面積を求めることについての知識・技能の習得に課題があると考えられる。
○ 指導改善の手立て
扇形に関しては、同一円の弧の長さがその中心角の大きさに比例することを理解して、扇形の弧の長さや面積を求めることができるようにすることが大切である。その際、扇形を作図する時間を確保し、作図した図形を基に、公式を用いて求めたり、比の考え方を利用して求めたりして、より理解が深まるようにする。日常生活の身近な題材であるピザやケーキ等を用いて、数学が日常生活で利用できることを実感させながら、技能の習熟を図っていく必要がある。
[中学2年生 大問9]
○ 問題の概要 |
 |
○ 解答状況
問9(2)は「おおむね達成」の期待正答率45.0に対して、正答率が40.3で、4.7ポイント下回り、問9(4)は「おおむね達成」の期待正答率50.0に対して、正答率が29.3で、20.7ポイント下回った。具体的な事象を式に表すこと、比例の意味、グラフ上の座標の意味や表し方についての理解が十分でなかったことが考えられる。
○ 指導改善の手立て
具体的な事象について式に表す際には、文字の代わりに具体的な数を当てはめて考察できるようにすること、また、簡単な表に表し、変化や対応の様子を考察することができるようにすることが大切である。グラフ上の座標については、式に具体的な数を代入しながら表を作成していく際に、表、式、グラフの相互の関連性をもたせた指導をする。特に、座標を求める際には、反比例の式を求めて、その式に x の値を代入して求めたり、表に表して反比例の特徴から求めたりすることができるようにする必要がある。このような複数の解き方がある問題を設定し、取り組ませることは、数学的な思考力、判断力、表現力を育むことにもつながると考えられる。
|
| |
|
| |
[中学3年生「A問題」 大問6]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率55.0に対して、問6(1)の正答率が40.4で14.6ポイント、問6(2)の正答率が45.8で9.2ポイント下回った。2つの直線が平行になるための根拠と多角形の内角の和を表す式の意味についての理解に課題があると考えられる。
○ 指導改善の手立て
多角形の内角の和を表す式が、多角形を三角形に分割することによって導くことができることを理解させる必要がある。三角形に分割する活動では、1つまたは2つの頂点から対角線を引いたり、三角形の内部、外部や辺上の点から各頂点に直線を引いたりして、いろいろな方法で三角形に分割することができることを実感させることが大切である。公式を導く際には、分割してできる三角形の個数を、もとの多角形の辺や頂点の数等と対応させて数え上げることによって、より理解を深めさせたい。多角形の内角の和を求める際には、計算の過程を振り返る活動として、式の意味を確認する活動を取り入れることも必要である。
[中学3年生「A問題」 大問12]
○ 問題の概要 |
 |
○ 解答状況
「おおむね達成」の期待正答率50.0に対して、正答率が38.1であり、11.9ポイント下回った。具体的な事象の中から、2つの数量を取り出し、数量の関係を式に表すことに課題があると考えられる。
○ 指導改善の手立て
具体的な事象の中から、2つの数量を取り出し、数量の関係を式に表すために、数量の関係を具体的な数を使って表に表したり、言葉の式や線分図等で表したりする活動を取り入れ、問題場面の理解を深められるように配慮する必要がある。
[中学3年生A問題 大問13]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率50.0に対して、正答率が37.6であり、12.4ポイント下回った。二元一次方程式の解を座標とする点の集合が、一次関数のグラフの直線となるという知識に課題があると考えられる。
○ 指導改善の手立て
二元一次方程式の解について、いくつかの x の値に、対応する y の値を求めさせ、それを座標とする点を座標平面上に表す活動を取り入れることが必要である。その際、 x や y の値が整数でない座標があることも確かめる場面を設定することが大切である。 |
| |
|
傾向3 |
数学的な表現を用いて説明することなどの記述式の学習内容に課題がある。
[中学2年生 大問3]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率40.0に対して、正答率が22.1であり、17.9ポイント下回った。与えられた事柄から数量の大小関係を読み取って、成り立つ数学的な事実について説明することに課題があると考えられる。
○ 指導改善の手立て
これまでの数値の大小関係から、数量の大小関係へと見方を変えていかなければならないことに配慮する必要がある。特に、式に表されている文字の式について、数量の関係を把握し、さらに大小関係を把握できるよう一つ一つ丁寧に指導する必要がある。その際、文字だけで考えるよりも、具体的な数に置き換えて考えさせる場面を数多く設定していきたい。これらの学習内容を通して、等号の他に不等号を用いることで、数量の大小関係を式に表したり、その意味を読み取ったりすることができることを理解できるようにし、数学的な見方や考え方を身に付けさせることが大切である。
[中学2年生 大問10]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率40.0に対して、正答率が20.8であり、19.2ポイント下回った。事柄が成り立つ理由を与えられた情報を基に説明することに課題があると考えられる。
○ 指導改善の手立て
新たに見いだした事柄を説明するためには、新たに見いだすために基になっている説明を振り返ることが考えられる。この問題は、時計の長い針の説明を基に、短い針の時間と角度の関係について説明をするものであった。そのため、短い針について説明する際に、基になっている長い針の説明と何が変わり、何が変わっていないかを明らかにしながら考えさせる必要がある。このように基になっている説明を振り返り、新しく見いだした事柄が成り立つか成り立たないかを説明することができるような場面を設定することは、数学的な思考力、判断力、表現力を育むことにつながると考える。
[中学3年生「B問題」 大問1]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率40.0に対して、正答率が13.4であり、26.6ポイント下回った。数学的に解釈したり、事柄が成り立つ理由を数学的な表現を用いて説明することに課題があると考えられる。
○ 指導改善の手立て
表、式、グラフ等から得られた数学的な結果を事象に即して解釈できるようにすることが大切である。指導に当たっては、文字式を用いて求めた後で、計算の過程を振り返る場面を設定することが考えられる。その際、計算の過程で消去された文字に注目し、その意味をもとの事象に即して考えさせる場面を取り入れ、消去された文字の値に関係なく決まると解釈する活動を取り入れる必要がある。ある事柄が成り立つ理由を説明する際に、説明すべき事柄とその根拠の両方を示し、数学的な表現を用いて説明できるような学習活動を数多く取り入れる必要がある。
[中学3年生「B問題」 大問5]
○ 問題の概要 |
 |
○ 解答状況
「おおむね達成」の期待正答率40.0に対して、正答率が24.8で、15.2ポイント下回った。問題解決の方法や手順を、数学的な表現を用いて説明することに課題があると考えられる。
○ 指導改善の手立て
AE=CEが成り立つことを説明するために、△ACEに着目し、△ACEが直角二等辺三角形または二等辺三角形になっていることに気付かせる必要があると考える。さらに、△ACEが直角二等辺三角形または二等辺三角形であることを説明するために三角形の内角の和が180°を利用していることにも気付かせる必要がある。このように長さを置き換えて考察することができるような課題に数多く取り組ませることによって、図形についての数学的な見方や考え方を高めることができると考える。また、図形領域の指導において、等しい辺や等しい角を説明する際に、どのような図形の性質などを根拠として利用しているかなどを説明する場面を取り入れる必要があると考える。 |
| |
|
| |
|
| エ |
これからの指導に向けて |
| |
今回の調査によって明らかになった指導改善のための重点項目は、次の通りである。
(ア)基礎的・基本的な知識・技能の習得を図ること。特に学習指導要領の移行措置により追加された学習内容や課題が見られる学習内容における知識・技能の習得を図ること。
(イ)基礎的・基本的な知識・技能を活用して問題を解決するために必要な思考力、判断力、表現力を育むこと。
以上の2つの重点項目を踏まえて、指導改善を図っていく必要がある。特に、日々の授業においては、授業のねらいを達成するために数学的活動を位置付けた授業展開や指導の手立ての工夫や改善を図っていくことが大切であると考える。
※数学的活動は、基礎的・基本的な知識及び技能を確実に身に付けるとともに、数学的に考える力を高めたり、数学を学ぶことの楽しさや意義を実感するために、重要な役割を果たすものである。
(ア) 基礎的・基本的な知識・技能の習得に向けて
「球や扇形に関すること」「相対度数を求めること」「中央値、最頻値、有効数字などの用語に関すること」などの基礎的・基本的な知識・技能の習得に課題があることが分かった。今後、これらの課題を解決するためには、数学的活動を位置付けた授業実践を積み重ねていくことが大切であると考える。数学的活動を位置付けた授業を行う上での配慮事項は以下の3つである。
○観察、操作や実験などの具体的な活動を通して、より理解が深まるような指導の充実。
○内容系統と関連性が少ない学習内容については、意図的に再度取り上げることによって、理解を深めたり拡げたりする指導の充実。
○数学の用語については、数学の用語の使い方に慣れることで、思考をより正確に、より的確に、より能率的に行うことができるようになるため、用語を用いることのよさを実感を伴って理解できるような指導の充実。
(イ)数学的な思考力、判断力、表現力を育むために
「数学的な表現を用いて説明すること」「与えられた情報を基に、成り立つ事柄を説明すること」などの数学的な思考力・判断力・表現力を問う問題に課題があることが分かった。数学的な思考力、判断力、表現力を育むためには、言語活動を重視した数学的活動を位置付けた授業実践を積み重ねていくことが大切であると考える。数学的活動を位置付けた授業を行う上での配慮事項は以下の3つである。
○試行錯誤をしたり、観察、操作や実験をしたりするなどの具体的な操作活動と考えたり説明したりする活動を結び付けた指導の充実
○新しく見いだした事柄、問題解決の方法や手順、事柄が成り立つ理由などについて自分の考えをまとめたり、他の人に分かりやすく説明したり、他の人の考えを理解したりする活動を取り入れた指導の充実
○身近な日常生活と結び付きのあるものや多様な見方や考え方ができるものなど、題材や課題についての設定を工夫した指導の充実。 |
| |
|
| |
|
| オ |
授業実践に参考となるリンク |
| |
|
| |
 |
| |
|
| |
 |