���w�I�����������ꂽ���ƓW�J�� |
|
|
|
|
|
�@�P���u�}�`�Ƒ����v�̏��P���u���s���Ɛ����̔�v�i�T���ԁj�ɂ����鐔�w�I�����������ꂽ���ƓW�J�Ăł��B |
| |
�P���@�}�`�Ƒ����@�i�[�ъفj
�@�Q�@���s���Ɛ����̔�
�@�@
�y�E�P�E�@���s���Ɛ����̔�z�@�@
�S�T����
|
| |
| |
|
�@�E�@���s���Ɛ����̔�Ɋւ��鐫���𗝉�����B
�@�E�@���s���Ɛ����̔�̐����𗘗p���āA�ӂ̒��������߂邱�Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
���ȏ�118�y�[�W�́u�Ƃт�̖��v�Ɏ��g�ށB |
| �� |
�{���̊w�K���e�u���s���Ɛ����̔�̊W�ɂ��Ċw�ڂ��v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
���ȏ�119�y�[�W�́u�Ђ낰�悤�v�Ɏ��g�ށB |
|
| ���荇�� |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA��APQ�Ɓ�ABC�������ɂȂ邱�Ƃ̏ؖ���b�������B |
| �� |
�O���[�v�̍l���\���A�ؖ����m�F����B |
| �� |
�����ɂȂ邱�Ƃ���AAQ�APQ�̒������m�F����B |
| �� |
���s���Ɛ����̔�ɂ��Ă܂Ƃ߂�B
��ABC�̕�AB�AAC��ɁA���ꂼ��A�_P�AQ������Ƃ��A
PQ//BC�Ȃ�A
AP�FAB��AQ�FAC��PQ�FBC
|
|
| �� |
���ȏ�119�y�[�W�̖�P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�l�̋��ߕ��ɂ��āA�����̍l��������������B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
�O���[�v�ŁA���ȏ�120�y�[�W�́u�����̂��Ƃœ`���悤�v��b�������B |
| �� |
�ؖ����m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���s���Ɛ����̔�ɂ��ăm�[�g�ɂ܂Ƃ߂�B |
|
|
|
|
|
�@�E�@���s���Ɛ����̔�Ɋւ��鐫���𗝉�����B
�@�E�@���s���Ɛ����̔�̐����𗘗p���āA�ӂ̒��������߂邱�Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
�O���̂܂Ƃ߂���ɁA���s���Ɛ����̔�̐����ɂ��Ċm�F����B |
| �� |
�{���̊w�K���e�u���s���Ɛ����̔�̊W�ɂ��Ċw�ڂ��v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�ۑ���l����B
��ABC�̕�AB�AAC��ɁA���ꂼ��A�_P�AQ������Ƃ��A
PQ//BC�Ȃ�AAP�FPB��AQ�FQC�ł��邱�Ƃ��ؖ����܂��傤�B |
|
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
��ABC���m�[�g�ɂ����A�ۑ�̏������m�F����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�ؖ���b�������B |
| �� |
�O���[�v�̍l���\���A�ؖ����m�F����B |
| �� |
���ȏ�121�y�[�W�̂܂Ƃ߂���ɁA���s���Ɛ����̔�ɂ��Ă܂Ƃ߂�B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�121�y�[�W�̖�Q���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�����Ƌ��ߕ����m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���s���Ɛ����̔�ɂ��Ă̂܂Ƃ߂���ɁA��̍l�����ɂ��Ċm�F����B |
|
|
|
|
|
�@�E�@���s���Ɛ����̔�̐������g���ďؖ����l���邱�Ƃ��ł���B
�@�E�@���s���Ɛ����̔�̐����𗘗p���āA�ӂ̒��������߂邱�Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
�O���̂܂Ƃ߂���ɁA���s���Ɛ����̔�ɂ��Ċm�F����B |
| �� |
�{���̊w�K���e�u���s���Ɛ����̔���g���ďؖ����悤�v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�ۑ���l����B
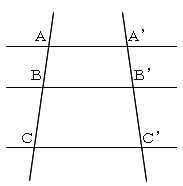
�Q�̒������A�R�̕��s�Ȓ���
�ƁA�}�̂悤�Ɍ�����Ă���Ƃ��A
�@�`�a�F�a�b���`�f�a�f�F�a�f�b�f
�@�ł��邱�Ƃ��ؖ����܂��傤�B
|
|
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
���������}�������A�ؖ����l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�ؖ���b�������B |
| �� |
�O���[�v�̍l���\���A�ؖ����m�F����B |
| �� |
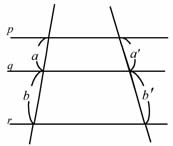
�ۑ�̏ؖ�����ɁA
�@
���� p�Aq�Ar �����s�̂Ƃ��A
�@�@a�Fb��a'�Fb'
�@ a�Fa'��b�Fb'
�����藧���Ƃ̐������A��������B |
 |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�122�y�[�W�̖�R�A��S���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�Ή����Ă���ӂ⋁�ߕ��ɂ��āA�����̍l��������������A�������m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���s���Ɛ����̔�ɂ��ăm�[�g�ɂ܂Ƃ߂�B |
|
|
|
|
|
�@�E�@�u�����̔�ƕ��s���v���u���s���Ɛ����̔�v�̋t�ɂȂ��Ă��邱�Ƃ𗝉�����B |
| �i�K |
|
| ���� |
| �� |
���ȏ�121�y�[�W�̕��s���Ɛ����̔�̂܂Ƃ߂���ɁA
�@
PQ//BC�Ȃ�AAP�FAB��AQ�FAC�ł��邱�Ƃ��m�F����B |
| �� |
�{���̊w�K���e�u�����̔�ƕ��s���̊W���w�ڂ��v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
AP�FAB��AQ�FAC�Ȃ�APQ//BC�����藧���\�z����B |
|
| ���荇�� |
| �� |
���ȏ�123�y�[�W�̖�T���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�ؖ���b�������B |
| �� |
�O���[�v�̍l���\���A�ؖ����m�F����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�121�y�[�W�̇A�̋t���l����B
| AP�FPB��AQ�FQC�Ȃ�APQ//BC�ł��邱�Ƃ��ؖ����܂��傤�B |
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�ؖ���b�������B |
| �� |
�O���[�v�̍l���\���A�ؖ����m�F����B |
| �� |
�`�o�F�o�a���`�p�F�p�b�Ȃ�A�o�p//�a�b�����藧���Ƃ𗝉�����B |
| �� |
���ȏ�124�y�[�W�̖�U���l����B |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
�e�ӂ̒�����p���āA
�@
AF �F AB�@���@AE �F AC
�@
BD �F BC�@���@BF �F BA
�@
CD �F CB�@���@CE �F CA
�ׂ�B |
�܂��� |
AF �F FB �� AE �F EC
BD �F DC �� BF �F FA
CD �F DB �� CE �F EA |
| �� |
���낢��ȋ��ߕ��Ɠ������m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
���Ƃ�U��Ԃ�A�����̔�ƕ��s���ɂ��ăm�[�g�ɂ܂Ƃ߂�B |
|
|
|
|
|
�@�E�@�u�����̔�ƕ��s���v���u���s���Ɛ����̔�v�̋t�ɂȂ��Ă��邱�Ƃ𗝉�����B
�@�E�@�����̔�ƕ��s���̐����𗘗p���āA�����������邱�Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
�{���̊w�K���e�u�����̔�ƕ��s���̐����𗘗p���āA�����������悤�v��m��B |
| �� |
�O���̏ؖ�����ɁA�����̔�ƕ��s���̐����K����B |
|
|
| ���ʂ� |
| �� |
���ȏ�124�y�[�W����ɁA�����̔�ƕ��s���ɂ��Ă܂Ƃ߂�B |
|
| ���荇�� |
| �� |
���ȏ�124�y�[�W�̖�V���l����B |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
���������}�������A���̐}����Ɂ�ABC�Ɓ�A'B'C'�������ɂȂ�킯���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����ɂȂ�킯�ɂ��āA�����̍l��������������B |
| �� |
�����̍l���\����B |
| �� |
�P�̓_�𒆐S�Ƃ��āA���낢��Ȑ}�`�̊g��}��k�}���������Ƃ��ł��邱�Ƃ�m��B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�125�y�[�W�̖�W�A��X���l����B |
| �� |
�O���[�v�ŁA�}���m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�����̔�ƕ��s���ɂ��Ă̂܂Ƃ߂�U��Ԃ�A�����̔�ƕ��s���̊W���m�F����B |
|
|
|
| |
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
|