���w�I�����������ꂽ���ƓW�J�� |
|
|
|
|
|
�@�P���u
�� y �� a x 2�v�̏��P���u�� y �� a x 2�v�i�R���ԁj�ɂ����鐔�w�I�����������ꂽ���ƓW�J�Ăł��B |
| |
�P���@�� y �� a x 2�@�i�[�ъفj
|
�@�P�@���ƃO���t
|
�@�@�y�E�P�E�@�� y �� a x 2�z�@�@
�S�R����
|
| |
| |
|
�@�E �@������ʂ��āA�Q�̐��ʂ̊W�����������A�ۑ�̉�����}�낤�Ƃ���B
�@�E�@�����肪�������͂��߂Ă���̎��ԂƗ������������ɒ��ڂ��A���ʂ̕ω���Ή���
�@
�l�q����A�Q��ɔ�Ⴗ��W�������������Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
���ɂ��Ă̊��K�̓��e�K����B |
| �� |
�{���̊w�K���e�u�Q�̐��ʊW�ɂ��čl���悤�v��m��B |
| �� |
��ʐݒ��m��B
���܂���400�N�قǑO�A�K�����C�Ƃ����l���A���̗̂����^���ɂ��ďڂ������ׁA���̂��������͂��߂Ă���̎��ԂƗ������鋗���̊W�ɂ��āA���锭�������܂����B
�����F�n�ʂɗ�����܂łɂR�b���������Ƃ����Ă���l�������B
���m�@�F�Ƃ������Ƃ́A���悻45���̂Ƃ��납�痎�����ˁB
�������F���`�A���ł���Ȃ��Ƃ��킩��́H
�@�@�@�@
���Ⴀ�A�P�b�Ԃ�15������������Ă��Ƃ��ˁH
|
|
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
����������̍l�������������ǂ�����\�z����B |
| �� |
�ۑ�P��m��B
������ʂ��āA�����肪�������͂��߂Ă���̎��� x (�b)�ƁA
������������ y (m)�𑪒肵�A2�̐��ʂ̊Ԃɐ��藧�W�ׂ܂��傤�B |
|
| �� |
�����肪�������͂��߂Ă���̎��ԂƁA�������������̊Ԃɐ��藧�W�ɂ��āA���ׂ���@���l����B |
|
| ���荇�� |
| ���w�I�����@�k�ώ@�A����Ȃǂ̋�̓I�Ȋ����l |
| �� |
�O���[�v�Ŏ������s���B |
| |
�@
�A
�B
�C
|
�q�����̕��@�r
�L�^�e�[�v���L�^�^�C�}�[�ɒʂ��A�������t����B�L�^�^�C�}�[�Ƃ̒�R���ł��邾�����Ȃ��Ȃ�悤�Ƀe�[�v�����B
�L�^�e�[�v�����l�͊��̏�ɏ��A�L�^�^�C�}�[�����l�͂�������Ǝ�ň���A�r�̈ʒu���Œ肷��B
�L�^�^�C�}�[�̃X�C�b�`�����A�����ɂ�����ƃe�[�v���肩�痣���B
�L�^�e�[�v�ɁA�U�œ_(0.1�b)���ƂɈ��t���A�͂��߂̈�̋����𑪂�B
�@�@�@�@�@
���@�e�O���[�v�łQ�`�R��������s���B |
| �� |
�����̌��ʂ�\��O���t�ɕ\���B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�\��O���t����C�t�����Ƃ�b�������B |
| �� |
�O���[�v���ƂɋC�t���\���A�S�̂Ŋm�F����B |
|
| �[�߂� |
| �� |
�ۑ�Q���l����B
���̕\�́A�{�[�����������͂��߂Ă���̎��� x (�b)�Ɨ������鋗�� y (m) �̊W��\�������̂ł��Bx �Cy �ɂ͂ǂ�ȊW�����邩�l���Ă݂܂��傤�B
 |
|
| ���w�I�����@�k�ڂ̑O�̉ۑ肩��A�����̖{�������������Ƃ��銈���l |
| �� |
�\�����A�� y ��a x 2 �ŕ\�������̓����������o���B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA�����̍l��������������B |
| �� |
y���T x 2 �ɂȂ邱�Ɗm�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�����̌��ʂ�ۑ�Q��U��Ԃ�A y��a x 2 �ŕ\�����������邱�Ƃ��m�F����B |
|
|
|
�q���H���I���ār
���@���w�I�����ɂ���
�E
������̗����̎�����ʂ��āA���k�͐g�̂܂��Ɋ�y��a x 2 �̊W�ɂ���Q�̐��ʂ�����Ƃ������ƂɊS�������A���̌�̊w�K�ӗ~�̌���ɂȂ���܂����B
�E�����Ȃǂ̐��w�I�����u�C�@�ώ@�A����Ȃǂ̋�̓I�Ȋ����v�������ꂽ���Ƃ��s���ۂ́A�����̑O�Ɏ������ʂ�ۑ�̗\�z����������A����ꂽ���ʂ���ɍl�@���s�����肷�邱�ƂŁA�w�K���e�̗����ɂ��Ȃ���Ɗ����܂����B�������A�����̌��ʂ���A���̊W����ʉ�������A���̉ۑ�ɂȂ����肷�邽�߂ɂ́A�Ȗ��Ȏ��ƌv�悪�d�v�ł��邱�Ƃ�������܂����B
���@�w�K�]���̐i�ߕ��ɂ���
�E
���w�ւ̊S�E�ӗ~�E�ԓx�̊ϓ_�ɂ��ẮA�O���[�v�ŁA�\��O���t����C�t�����Ƃ�b����������(�ڍ��ƓW�J�Ă��w�K�����̂W)�ŕ]�����s���A�����̌��ʂ���ɂ����ۑ�ւ̎�g�̏������܂����B���ۂɍs���������̌��ʂ���ɁA�ۑ�Ɏ��g���߁A�قƂ�ǂ̐��k���u�����ނ˖����ł���v(�a)�ɒB���邱�Ƃ��ł��܂����B
�E
���w�I�Ȍ�����l�����̊ϓ_�ɂ��ẮA�ۑ�Q���l���銈��(�ڍ��ƓW�J�Ă̊w�K�����̂X)�ŕ]�����s���܂����B�u�����ނ˖����ł���v(�a)�ɒB���Ă��Ȃ����k�ɂ̓q���g�J�[�h��z�t���A x 2 �̒l�̕ω��� y �̒l�Ƃ̊W�ɒ��ڂ��čl����Ȃǂ̏������s�������ƂŁAx �� y �̊W�� y���T x 2 �ƂȂ邱�ƂɋC�t�����k�����܂����B
|
|
|
�@�E�@�� y��a x 2 �̒l�̕ω���Ή���\�ɂ���Ē��ׁA���̓������l���邱�Ƃ��ł���B
�@�E�@�� y��a x 2 �̈Ӗ��𗝉�����B
|
| �i�K |
|
| ���� |
| �� |
�O���̊w�K��U��Ԃ�Ay��a x 2 �ŕ\�����������邱�Ƃ��m�F����B�@
|
| �� |
�{���̊w�K���e�u�� y��a x 2 �̕ω��̓�����m�낤�v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
�ۑ�P���l����B
�{�[�����Ζʂ����낪��͂��߂Ă���̎��Ԃ�x�b�A���̊Ԃɂ��낪�鋗���� y���Ƃ��܂��B����ΖʂŃ{�[�������낪���ƁAx �� y �̊W�́A���̕\�̂悤�ɂȂ�܂����Bx �� y �̊W�ׂ܂��傤�B
 |
|
|
| ���荇�� |
| �� |
x �� y �̊W�ɂ��Ċm�F����B |
| �� |
x �� y �̊W���A y��a x 2 �̌`�ŕ\�����������邱�Ƃ𗝉�����B |
| �� |
���ȏ�82�y�[�W�̖�P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����̍l��������������A�������m�F����B�@
|
| �� |
���ȏ�83�y�[�W�̗�P����ɁAx �� y �̊W���A y���T x 2 �ƂȂ邱�Ƃ𗝉�����B |
| �� |
���ȏ�83�y�[�W�̖�Q���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����̍l��������������B |
| �� |
�S�̂œ������m�F����B |
|
| �[�߂� |
| �� |
���ȏ�83�y�[�W�́u�Ђ낰�悤�v�Ɏ��g�ށB |
| �� |
�ۑ�Q���l����B
�� y���R x 2 �ɂ��āA
| �@ |
x �̒l�� n�{����ƁAy �̒l�͉��{�ɂȂ�܂����B |
| �A |
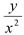 |
�̒l�ɂ͂ǂ�ȓ���������܂����B |
|
|
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����̍l��������������B |
| ���w�I�����@�k�ڂ̑O�̉ۑ肩��A�����̖{�������������Ƃ��銈���l |
| �� |
�� y��a x 2 �̓������܂Ƃ߂�B
| �E |
�� y��a x 2 �ɂ��āAx �̒l�� n�{����ƁAy �̒l�� n2 �{�ɂȂ�B |
| �E |
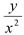 |
�̒l�����ŁAa�ɂȂ�B |
|
|
| �� |
y �� x �̂Q��ɔ�Ⴗ��W�ɂ��Ēm��B
x�Cy �̊W���Ay��a x 2�ŕ\�����Ƃ��A
y �� x �̂Q��ɔ�Ⴗ��Ƃ����B�@�@�@a�͔��萔 |
|
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�܂Ƃ߂����Ȃ���A�� y��a x 2 �̓������m�F����B |
|
|
|
|
|
�@�E�@y �� x �̂Q��ɔ�Ⴗ��W���A���ɕ\�����Ƃ��ł���B |
| �i�K |
|
| ���� |
| �� |
�O���̂܂Ƃ߂����Ȃ���A�� y��a x 2 �ɂ��ĕ��K����B |
| �� |
�{���̊w�K���e�ux�Cy �̊W�����ɕ\�����v��m��B |
|
|
| ���ʂ� |
| ���w�I�����@�k���藧������\�z���銈���l |
| �� |
���ȏ�84�y�[�W�̗��P�ɂ��āA�����̕��@��\�z����B |
|
| ���荇�� |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA�����̕��@�ɂ��āA�����̍l��������������B |
| �� |
�S�̂ŋ��ߕ��Ɠ������m�F����B |
| �� |
���ȏ�84�y�[�W�̖�R���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�ŁA���ߕ��Ɠ������m�F����B |
|
| �[�߂� |
| ���w�I�����@�k���W�I�ɍl���銈���l |
| �� |
���ȏ�84�y�[�W�̗��K���P���l����B |
| ���w�I�����@�k�����̍l����l�ɓ`���銈���E�l�̍l���𗝉����銈���l |
| �� |
�O���[�v�̃����o�[�Ō݂��ɁA���ߕ��ɂ��āA�����̍l��������������B�@
|
| �� |
�S�̂ŁA���ߕ��Ɠ������m�F����B |
|
| �܂Ƃ߂� |
| ���w�I�����@�k�������s����������U��Ԃ銈���l |
| �� |
�� y��a x 2 �̎��̋��ߕ��ɂ��ĐU��Ԃ�A�m�[�g�ɐ�������B |
|
|
|
| |
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
|

