|
|
|
単元「変化と対応」の小単元「比例のグラフ」(3時間)における数学的活動を取り入れた授業展開案です。 |
| |
単元 変化と対応 (啓林館)
2 比例
【・3・ 比例のグラフ】
全3時間
|
| |
| |
ねらい |
・比例の関係をグラフに表すことができる。
・比例の関係 y =ax のグラフの特徴を理解する。 |
| 段階 |
|
| つかむ |
| ○本時の学習内容「比例の関係をグラフの特徴を見つけよう」を知る。 |
|
|
| 見通す |
| ●比例の関係 y =2x がどのようなグラフになるか予想する。 |
|
| 練り合う |
| ●比例の関係 y =2x の式を基に、対応する x 、 y の値を求めた表を作成する。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● y =2x がどのようなグラフになるか、表とグラフを基に自分の考えをグループで説明し合う。 |
| ○ x の値を小数にとり、細かくグラフの様子を見る。 |
| ○比例の関係 y =2x のグラフについて説明を聞く。 |
|
| 深める |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●自分の考えを基に、どのようなグラフになるか説明し合う。 |
| 数学的活動 〔目の前の課題から、物事の本質を見抜こうとする活動〕 |
| ●比例の関係 y =2x と y =−2x のグラフからその特徴をグループで話し合う。 |
|
| まとめる |
| ●比例の関係のグラフの特徴(原点を通る直線である)をノートに整理する。 |
|
|
|
|
ねらい |
・比例の関係の式からグラフをかくことができる。
・比例定数の値により、グラフが異なることを理解する。
|
| 段階 |
|
| つかむ |
| ○本時の学習内容「比例の関係のグラフを工夫してかこう」を知る。 |
| ○課題1を考える。 |
| 比例の関係 y =−3x のグラフを簡単にかく方法を見つけよう。 |
|
|
|
| 見通す |
| ●比例のグラフの特徴を基に、グラフのかき方を予想する。 |
|
| 練り合う |
| ○比例のグラフの特徴から、原点以外の点を1つ決めればよいことを確認する。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
●互いの考えをグループ内で説明し合う。また、解決方法を発表し、全体で話し合
う。 |
|
| 深める |
| 比例の関係 |
y= |
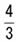 |
x |
のグラフを簡単にかく方法を見つけよう。 |
|
|
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●比例定数が分数のときのグラフのかき方を話し合う。 |
| ●全体の場で、そのグラフのかき方を発表し、確認する。 |
|
| まとめる |
| ●比例の関係のグラフの簡単なかき方をノートに整理する。 |
|
|
|
|
ねらい |
・比例の関係で、変域のあるグラフをかくことができる。
|
| 段階 |
|
| つかむ |
| ○教科書110ページのまとめを基に、グラフの特徴やかき方を復習する。 |
| ○本時の学習内容「変域のある場合のグラフについて考えよう」を知る。 |
|
|
| 見通す |
|
| 練り合う |
| ○ x の変域が 0≦ x ≦3 となることを確認する。 |
| ○ x 、 y の関係を表す式とグラフについて考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
●互いの考えをグループで説明し合う。また、解決方法を発表し、全体で話し合
う。 |
| ○式を確認し、変域がある場合のグラフのかき方を理解する。 |
|
| 深める |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ●式とグラフについて、グループで自分の考えを説明し合う。 |
|
| まとめる |
| ●変域のある場合のグラフのかき方で、気を付けることをノートに整理する。 |
|
|
|
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
最終更新日:2012-11-30 |
|