過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
[問題]
A、B2台の自動車があります。Aの自動車は、35Lのガソリンで700㎞、Bの自動車は、50Lのガソリンで800㎞走れます。
ガソリンの量と走る道のりについて、AとBを比べましょう。 |
|
|
| ○ |
燃費の意味をとらえるために、自動車の話をしてイメージさせる。 |
| ○ |
どちらか一方をそろえれば比較することができることをおさえるために、前時の学習を想起する。 |
| ○ |
単位量あたりの大きさで比べるために、公倍数では見つけにくかったり、数が大きくなったりすることに気付かせる。 |
|
ガソリンの量か走る道のりのどちらかをもとにして比べてみよう。
|
|
見通す |
|
| ○ |
| ガソリンの量、道のりのどちらかを「1」にそろえて比 べると比較できることに気付かせる。 |
|
|
| 自力解決 |
3 |
自力解決をする。
《予想される児童の考え》
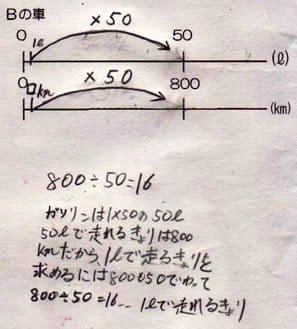
①ガソリンの量を1Lにそろえて考える方法
A 700÷35=20 1Lで20㎞走る
B 800÷50=16 1Lで16㎞走る
だから、Aの方がよく走る
②道のりを1㎞にそろえて考える方法
A 35÷700=0.05 1㎞で0.05 L
B 50÷800=0.0625 1㎞で0.0625 L
だから、Aの方がよく走る
|
|
| ◎ |
| 説明するときに友達によく伝わるように、自分が何をそろえて比べているか、説明のポイント(根拠となるところや、何を求めているかが分かる部分)に線をひかせる。(ア) |
|
| ○ |
一つの方法で求めたら、他の方法も考えさせる。 |
| ◎ |
学び合いの活動で友達に説明させるために、ワークシートに図、式、言葉などを用いて記述するようにさせる。
(ア)
|
| ◇ |
どちらを単位量あたりにして表しているかを理解している。
【数量や図形についての知識・理解】[観察、ノート] |
|
|
| 学び合い |
|
| ◎ |
自分の考えを説明する際には、ワークシートを示しながら説明させる。(イ) |
| ◎ |
はじめに、自分の考えを伝え、どうしてそのように考えたか図や式、言葉等を関連付けながら説明させる。(イ) |
| ○ |
考えを深めるために、自分の考えと同じか違うかを意識させながら話し合わせる。また、よく分からないところは、お互いに質問し合うようにさせる。 |
| ○ |
自分と異なる考えについては、ノートにメモをとらせる。 |
|
5 |
解決方法を発表し、全体で話し合う。
|
| |
≪児童が実際にノートにかいた考え≫ |
|
|
 |
 |
|
|
◎ |
答えだけではなく、図や式、言葉などを関連付けながら説明させる。(イ) |
◎ |
考えを共有するために、一人に全てを発表させずに、続きを予想させたり、他の児童に発表させたりする。(イ) |
| ○ |
道のりを単位量あたりの大きさにして求めると、数値が小さくなっている方が、より燃費がよいことを捉えさせる。 |
| ○ |
単位量あたりの大きさで表すと、簡単にどんな時も求められることを理解させる 。 |
| ◇ |
単位量あたりの大きさで考え、どちらの車の燃費がいいかを比べることができる。
【数量や図形についての技能】[観察、ノート] |
|
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
異なった2つの量で表された大きさを比べるときは、単位量あたりの大きさを調べて比べると、簡単に比べられる。 |
| 7 |
振り返り問題を解く。
[問題]
みのるさんの畑とゆたかさんの畑の面積とじゃがいものとれた量は表の通りです。 どちらの方がよくとれたといえますか?
式や図、言葉を使って説明しましょう。
| |
みのる |
ゆたか |
| 面積(㎡) |
50 |
80 |
| とれた量(㎏) |
63 |
108 |
|
|
| 8 |
本時の学習で学んだことを算数日記に書く。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
|
| ○ |
単位量あたりの大きさで表すと、どんな数値であっても求められることを確認する。
|
|
○
|
活動が停滞している児童には、学び合いの段階で出てきた図や数直線を参考にして、わり算で求められることを理解させて取り組ませる。 |
|
|
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
|
