�ߒ� |
|
�w����̗��ӓ_�i�E�j�A�]���K���ƕ]�����@�i�����j
�Z���I�����i���j�A�h�b�s�����p�i���j |
���� |
[���]
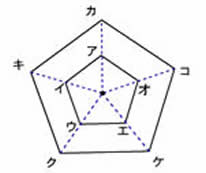
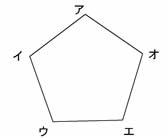
�܊p�`�A�C�E�G�I�̂Q�{�̊g��}�A�܊p�`�J�L�N�P�R�������܂��傤�B
|
|
�E |
����܂łɊw�K���������ȎO�p�`�̂�������A�P�̓_�𒆐S�ɂ�����������U��Ԃ�B |
�E |
�{���́A�ǂ̂悤�Ȃ������ł�����������₢�A�P�̓_�𒆐S�ɂ����g��}�̂������ɏœ_������B |
|
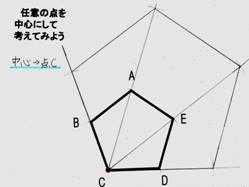
�P�̓_�𒆐S�ɂ����܊p�`�̊g��}�̂��������l���悤�B |
|
| ���ʂ� |
| �Q |
�����̌��ʂ������B |
| |
�s�\�z����鎙���̍l���t
�E�R���p�X���g���B
�E�Ίp�������ɂЂ��B
�E�P�̓_�𒆐S�Ɏ��B |
|
�E |
�P�̓_�𒆐S�ɂ����g��}�̂�������U��Ԃ�A��������u���S�Ƒ��̒��_���Ō��ԁv�Ȃǂ̌��t�������o���B |
|
| ���͉��� |
| �R |
���͉���������B |
| |
�s�\�z����鎙���̍l���t
�@�@���S�ƂȂ�_�����߂�B
�A�@���S�ƂȂ�_����e���_�֕⏕���i�Ίp���j���Ђ��B
�B�@�R���p�X�łQ�{�ɂȂ�ꏊ�ɓ_���Ƃ�B
�C�@�Q�{�ɂȂ�ꏊ�ɂƂ����_�ǂ������Ō��ԁB
|
|
|
|
| �� |
�P�̓_�𒆐S�ɂ��āA�g��}����������B �i�A�j�@ |
�E |
�Q�{�Ɋg�債���}���������V�[�g���������Ă����A�ł����������m�F�ł���悤�ɂ��Ă����B |
�E |
�P�̕��@�ō�}�ł��������ɂ́A��}�̎d���̐������������A���̕��@�ł���}�ł��Ȃ����l��������B |
���@�R���p�X���K��p���āA �P�̓_�𒆐S�ɂ������p�`�̊g��}���������Ƃ��ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�y�Z�\�z�i�m�[�g�j
�`�@�P�̒��_����̕⏕���i�Ίp���j��C�ӂ̓_����̕⏕�����Ђ��Ē��_���Ƃ�A�Q�ȏ�̂������Ŋg��}���������Ƃ��ł���B
�a�@�P�̒��_����̕⏕�����Ђ��Ē��_���Ƃ�A�g��}���������Ƃ��ł���B
�k�u�w�͂�v����v�iC�j�Ɣ��f���������ւ̎w���l
�@
�O���̍�}�̎d����U��Ԃ点�A���_���P���߂ĕ⏕�����Ђ�����B |
| �� |
��S���̎O�p�`�̏k�}�̂������ŁA�u�w�͂�v����v�iC�j�ł������������u�����ނ˖����ł���v�iB�j�ƂȂ�悤�w������B�܂��A�{���ɂ����āu�\�������ł���v�iA�j�ɂȂ�������������L�^�Ɏc���B |
|
| �w�э��� |
�S |
�����̍l�����O���[�v�Ő����������B |
|
�E |
��}�����}�`�������Ȃ�������������B |
|
| �� |
�P�̓_�𒆐S�ɂ����g��}�̂�����������������i�C�j |
�E |
��}�����}�`�����Ƃɐ��������A���������Ԉ���Ă��Ȃ������݂��Ɋm���߂�����B |
|
�T |
�l�������Ƃ��O���[�v�̑�\�����\���A�S�̂Řb�������B |
| �@�s���\���������̍l���t |
|
| �� |
����J������p���Ď����̃m�[�g���g����A���̐}���g���č�}�̎d�������������B |
| |
|
| �� |
��������ۂɂ́A��}�����}���w���Ȃ����}�̎菇��������悤�ɐ���������B�i�C�j |
�E |
�P�̓_�𒆐S�ɂ������p�`�̊g��}�̍�}�ɂ��A���K�̊g��}��k�}�̐��������p���Ă��邱�Ƃ��m�F����B |
|
| �܂Ƃ߂� |
|
�⏕�����Ђ��A�P�̓_�𒆐S�ɂ��đ��p�`�̊g��}���������Ƃ��ł���B
|
[���]
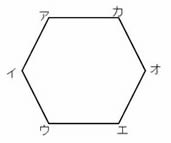
���̘Z�p�`�A�C�E�G�I�J���Q�{�̊g��}�������܂��傤�B
 |
| �W |
�{���̊w�K���Z�����L�ɂ܂Ƃ߂�B |
| |
�s���������ۂɏ������Z�����L�̗�t |


|
| �� |
�d�q����p���āA�������̊g��}���Љ�A���S�ɂȂ�_���ǂ��Ɏ���Ă��Q�{�̊g��}���������Ƃ��ł��邱�ƂɋC�t������B
|
�E |
�O�p�`����ɂ��Ȃ���P�̓_�𒆐S�ɂ��āA���p�`�̊g��}�����������Ƃ��܂Ƃ߂�B |
�E |
���S�ɂȂ�_����点�A�Z�p�`�̊g��}����������B |
| |
|
| �� |
�K�p���ɂ����Ă��A�{���̕]���K���ɏƂ炵�ĕ]�����s���A���͉����Łu�w�͂�v����v�iC�j�ł������������A���Ƃ�ʂ��č�}�̎d���𗝉��������ł��Ă���A�u�����ނ˖����ł���v�iB�j�ƕ]������B
|
�E |
���Ƃŕ����������Ƃ⊴�z�A���ꂩ��C��t���������Ƃ�X�ɒ��ׂĂ݂������ƂȂǂ���������悤�ɂ���B |
|