過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
[問題]
12:18を、それと等しい比で、できるだけ小さな整数の比になおすことを考えよう。 |
|
| ○ |
既習事項を活用させるために、前時を振り返り、等しい比の定義と性質を確認させる。
|
|
|
|
見通す |
2 |
解決の見通しをもつ。 |
| |
・ |
等しい比の性質を使う。 |
| |
・ |
比の値を使う。 |
|
| ◎ |
等しい比の定義と性質といった根拠を明らかにして考えさせる。(ア) |
|
| 自力解決 |
3 |
自力解決をする。 |
| |
《予想される児童の考え》 |
| |
① |
等しい比の性質を使う。
両方の数を2でわって
12:18=6:9 |
|
| |
② |
等しい比の性質を使う。
両方の数を6でわって
12:18=2:3 |
|
| |
③ |
比の値を使う。 |
|
| |
|
比の値は、 12÷18= |
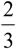 |
| |
|
だから 12:18=2:3 |
|
|
| ◎ |
この後の学び合いの活動で友達に説明させるために、ノートに図、式、言葉などを用いて記述するようにさせる。(イ) |
|
| 学び合い |
|
| ◎ |
自分の考えを説明する際には、ノートを示しながら説明させる。(イ) |
| ◎ |
自分の考えを説明させる際には、児童が発言する次のような言葉に注目し、児童の考えをつなげていく。 (イ) |
| |
・まず…自分の考えを分割し、整理しようする言葉。
・でも…反例をあげ、考えを説明しようとする言葉。
・だったら…友達の考えを基にして、その先を考えて
説明しようとする言葉。
・もし…条件を変えたり、考えを整理したり、一般化
を図ったりしようとする言葉。 |
| ◎ |
これまでの学習を基に、言葉や図、式などを関連付けて説明させる。(イ) |
| ◎ |
自分のやり方と同じか違うかを意識させながら聞かせる。また、よく分からないところは、お互いに質問し合わせる。(イ) |
| ◎ |
説明を聞いて、自分の考えと異なる考えやよい考えがあったらノートにかかせる。(イ) |
◇ 等しい比の性質を利用して、できるだけ小さな整数の比にすることができる。
【数量や図形についての技能】[ノート、行動観察] |
|
5 |
考えたことをグループの代表が発表・板書し、全体で話し合う。
|
| |
≪児童が実際にノートにかいた考え≫ |
 |
「①の考えのノート例」 |
| |
① |
両方の数を2でわって、さらに3でわる。
12:18=6:9=2:3 |
| |
② |
両方の数を6(最大公約数)でわって
12:18=2:3 |
| |
③ |
比の値を使う。
比の値は、12÷18=
だから 12:18=2:3 |
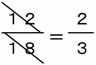 |
| |
・ |
①、②、③とも最小公倍数の6でわっている。 |
|
| ○ |
①と②を比べさせることで、12:18と等しい比は、いくつもあることをとらえさせる。それらの中で一番分かりやすい比が、2:3であることから、できるだけ小さな整数の比になおす意味を見出させる。
|
| ○ |
③は、最後まできちんと約分しなければ不十分な解答となり(①へとつながる)、最後まできちんと約分することで(②へとつながる)できるだけ小さな整数の比になおす意味を理解させる。また、わる数は、どんな数(最大公約数)になっているか考えさせる。 |
| |
|
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
・ |
「等しい比で、できるだけ小さな整数の比になおすことを、比を簡単にするという」
|
| 7 |
振り返り問題を解く。
(教科書p.65 ⑥⑦⑧) |
| 8 |
本時の学習を算数日記にまとめる。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
|
| |
|
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
|
