�ߒ� |
�w�@�K�@���@��
|
�w����̗��ӓ_�i�E�j�A�]���K���ƕ]�����@�i�����j
�Z���I�����i���j�A�h�b�s�����p�i���j |
���� |
[���]
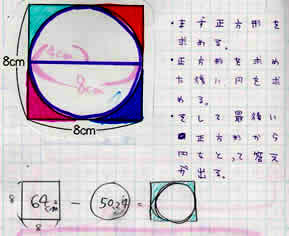
���̐}�`�̐F��t���������̖ʐς����߂܂��傤�B
|
|
�E |
�O���̊w�K��U��Ԃ�A�~�̖ʐς́A���a�~���a�~3.14�Ōv�Z���邱�Ƃ��m�F����B |
| |
|
| �� |
�d�q����p���Ė��̐}����A�ۑ�𑨂�������B |
|
�~�̖ʐς̌������g���āA�ʐς����߂悤�B |
|
| ���ʂ� |
|
�E |
���̐}�`����~�������������Ƃ��ł��邱�ƂɋC�t������B |
�E |
(1)�̐}�`�͉~�� 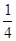 �ɂȂ��Ă��邱�Ƃ���̕��Ŋm�F����B �ɂȂ��Ă��邱�Ƃ���̕��Ŋm�F����B |
�E |
(2)�̉~�̒��a�͂W�p�ɂȂ邱�Ƃ��m�F����B |
|
| ���͉��� |
| �R |
���͉���������B |
�E |
�~�̖ʐς̌�����p���āA�}�`�̐F��t���������̖ʐς����߂�B |
�E |
�ʐς̋��ߕ���}�⎮�⌾�t�Ȃǂ�p���Ă����B |
|
�E |
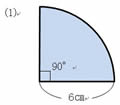
(1)�͉~��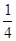 ������A���a�U�p�̉~�̖ʐς����߂Ă��� ������A���a�U�p�̉~�̖ʐς����߂Ă��� 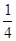 �ɂ���悢�B �ɂ���悢�B
�@�U�~�U�~3.14��113.04
�@113.04���S��28.26�@�@�@�@
�@�@�@�@�@�@�@�@�@
�����@28.26c�u |
�E |
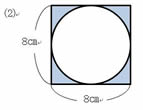
(2)�͂P�ӂ��W�p�̐����`�̖ʐς���A���a�S�p�̉~�̖ʐς��Ђ��Ƃ悢�B
�@
�W�~�W��64
�@
�S�~�S�~3.14��50.24
�@ 64�|50.24��9.76�@
�@�@�@�@�@�@�@�@
�@�����@50.24c�u |
|
| �� |
�ǂ̂悤�ɂ��ċ��߂�����������悤�ɁA�l���̍�����}�⎮�⌾�t�Ȃǂ�p���ăm�[�g�ɂ�������B�i�A�j |
�E |
(2)�̐����`����~��������c��̕����ɂ��ẴC���[�W�����ĂȂ������ɂ́A��̕��𑀍삳���čl��������B |
| |
|
���@�~�̖ʐς̌�����p���āA�~���܂ޕ����}�`�̖ʐς����߂邱�Ƃ��ł���B�y�Z�\�z(�ώ@�A�m�[�g)
�`�@�~�̖ʐς̌�����p���āA(�P)��(�Q)�̂ǂ���̐}�`�̖ʐς����߂邱�Ƃ��ł���B
�a�@�~�̖ʐς̌�����p���āA(�P)�܂���(�Q)�̂ǂ��炩�̐}�`�̖ʐς����߂邱�Ƃ��ł���B
�k�u�w�͂�v����v��(�b)�Ɣ��f���������ւ̎w���l
�@
�p�\�R����p����
�q���g�ƂȂ�悤�ȃA�j���[�V�����������A���̐}����ɗ���������B |
| �� |
�w�K�����̊ώ@����ƌ�̃m�[�g�L�q�̕��͂���ɁA�S����ΏۂƂ����]�����s���L�^�Ɏc���B |
|
| �w�э��� |
�S |
�����̍l�����O���[�v�Ő����������B |
�E |
�ʐς̋��ߕ��ɂ��Ď��Ɛ}���֘A�t���Đ�������B |
| |
|
| |
�u�菇�������Ȃ�������������l�q�v |
| |
|
| |
�s�������m�[�g�ɂ������l���t |
|
|
| �� |
���ꂼ��������}�`�̂ǂ̕��������߂Ă���̂���}�Ŋm�F�����A���Ɛ}���֘A�t���Đ���������B�i�C�j |
| |
|
�E |
�~�̖ʐς̌�����p���Ă��邩���m�F�����Ȃ���A�F�B�̐���������B |
|
�T |
�S�̂ŁA�~�̖ʐς̌�����p���Ėʐς����߂����Ƃɂ��Ęb�������B |
| |
|
| �� |
�d�q����p���Ď����̃m�[�g���g����A������g���Ȃ������������B |
�E |
�}����ɁA���a�̒������m�F�����A�ǂ���̖����~�̖ʐς̌�����p���ċ��߂Ă��邱�Ƃ��m�F����B |
�E |
�~������Ƃ����l������S�̂���~�̖ʐς����Ƃ����l�������g���Ă��邱�Ƃ��m�F����B |
|
| �܂Ƃ߂� |
| |
�}�`�̒��ɉ~�����t���āA�~�̖ʐς̌������g���čl����Ƃ悢�B |
[���]
���̐}�`�́A
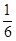 �̉~�ł��B�ʐς����߂܂��傤�B �̉~�ł��B�ʐς����߂܂��傤�B
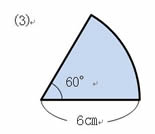
|
|
�s�������m�[�g�ɂ������l���t |
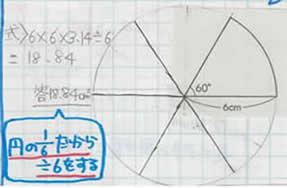 |
| �u�\�������ł���v��(�`)�Ɣ��f�����m�[�g�L�q�̗� |
�W |
�{���̊w�K���Z�����L�ɂ܂Ƃ߂�B |
| |
�s���������ۂɏ������Z�����L�̗�t |
| |
  |
|
�E |
�~�̖ʐς̌�����p���邱�Ƃɂ��Ă܂Ƃ߂�B |
�E |
���̐}�`����A�~��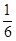 �ɂȂ��Ă��邱�Ƃ��m�F����B �ɂȂ��Ă��邱�Ƃ��m�F����B |
| |
|
���@�~���܂ޕ����}�`�̖ʐς��A�~�̖ʐς̌�����p���ċ��߂��邱�Ƃ𗝉����Ă���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�y�m���E�����z�i�ώ@�A�m�[�g�j
�`�@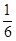 �̉~�ł��邱�Ƃ���ɁA������p���ĉ~�̖ʐς����߂���ɂU�������A���t�ł��ʐς̋��ߕ��ɂ��ċL�q���Ă���B �̉~�ł��邱�Ƃ���ɁA������p���ĉ~�̖ʐς����߂���ɂU�������A���t�ł��ʐς̋��ߕ��ɂ��ċL�q���Ă���B
�a�@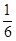 �̉~�ł��邱�Ƃ���ɁA������p���ĉ~�̖ʐς����߂���ɂU�������Ă���B �̉~�ł��邱�Ƃ���ɁA������p���ĉ~�̖ʐς����߂���ɂU�������Ă���B
�k�u�w�͂�v����v��(�b)�Ɣ��f���������ւ̎w���l
�@
�~�̖ʐς̌����Ɣ��a�̒������m�F�����A�~�������ɕ�����悢���l��������B |
| �� |
�u�w�͂�v����v��(�b)�ł��鎙�����u�����ނ˖����ł���v��(�a)�ƂȂ�悤�w�����A�{���ɂ����āu�\�������ł���v��(�`)�ɂȂ�������������L�^�Ɏc���B |
�E |
���Ƃŕ����������Ƃ⊴�z�A���ꂩ��C��t���������Ƃ�X�ɒ��ׂĂ݂������ƂȂǂ���������悤�ɂ���B |
|