平成22年度「全国学力・学習状況調査」の結果とこれからの指導に向けて
|
平成22年4月20日に実施された「全国学力・学習状況調査」の報告書・集計結果が7月末に文部科学省から提供されました。この結果と県独自の採点による結果を基に、本県におけるこれからの指導について提案します。具体的には、設問ごとの分析結果とこれからの指導に向けて、主に教科に関する調査(主として知識に関するA問題、主として活用に関するB問題)の結果とともに、その改善策について紹介します。
なお、平成22年度の結果については、県独自の採点によるものですが、平成20・21年度の結果については文部科学省から提供されている該当年度の「全国学力・学習状況調査」の報告書・集計結果によるものです。 |
| 平成22年度「全国学力・学習状況調査」の佐賀県小学校算数(6年生)の調査結果について |
| 評価の観点別の結果を見ると、活用に関するB問題や数学的な見方や考え方に課題があります。これは、平成20〜21年度の傾向とほぼ変わりません。
また、内容・領域別の結果についても、知識に関するA問題よりもB問題に課題があるといえます。 |
| ○ 評価の観点別の結果(佐賀県の正答率) |
| |
平成22年度 |
平成21年度 |
平成20年度 |
| |
|
|
|
|
|
| 数学的な見方や考え方 |
− |
38.7 |
− |
43.2 |
− |
39.6 |
算数的な表現・処理 |
81.1 |
80.2 |
77.5 |
75.1 |
83.1 |
71.3 |
数量、図形などについての知識・理解 |
65.4 |
52.5 |
81.3 |
− |
66.8 |
− |
|
○ 内容・領域別の結果(佐賀県の正答率) |
|
平成22年度 |
平成21年度 |
平成20年度 |
| |
|
|
|
|
|
数と計算 |
72.5 |
51.0 |
82.9 |
53.3 |
78.0 |
64.3 |
量と測定 |
72.6 |
35.6 |
79.9 |
57.4 |
56.7 |
50.0 |
図形 |
83.1 |
40.4 |
82.3 |
55.1 |
72.2 |
58.1 |
数量関係 |
63.9 |
53.7 |
61.9 |
54.0 |
72.3 |
42.9 |
|
| ○佐賀県全体の結果(設問別正答率及び無解答率) |
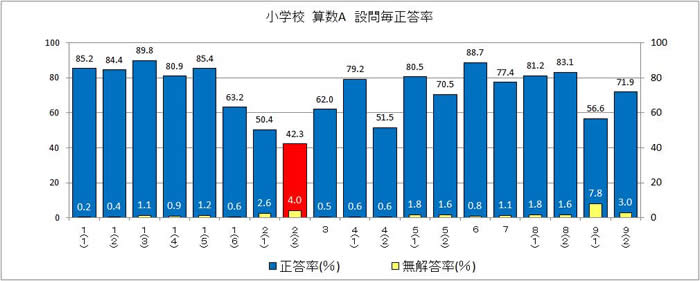
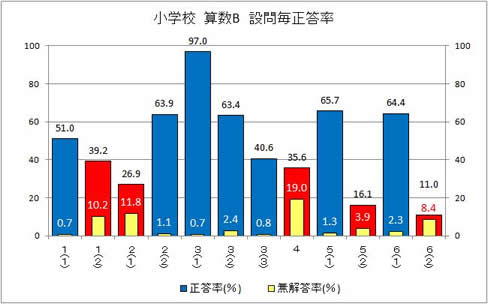
|
全国調査の佐賀県全体の設問別正答率で、特に正答率が低いものや無解答率が高いものを赤色で示しています。この赤色で示した課題が見られる設問について、以下に指導の工夫改善を提案します。
佐賀県教育センターでは、知識・技能の定着をサポートする学習プリントや活用にかかわる学習プリントを定期的に作成し、提供しています。ぜひご覧になり、ダウンロードして使っていただけたらと考えています。 |
|
設問ごとの分析結果とこれからの指導に向けて 【主として知識に関するA問題】
|
設問番号
2(2)
(数と計算)
正答率
42.3
無解答率
4.0
|
〔設問の概要〕…2L(リットル)のジュースを3等分したときの1つ分の量を分数で表わす。
〔出題の趣旨〕…除法の意味について理解している。 |
〈分析結果と課題〉
この問題では、被除数に当たる数と除数に当たる数を判断することが求められます。数量を等分したときの1つ分を求めるために除法が用いられることや商を分数で表せることの理解に課題があります。これは、「(整数)÷(整数)」の除法において、被除数の方が除数より大きくなると考え、式を3÷2と考えて商を3/2と解答したり、2÷3と立式しても、被除数を分母に除数を分子にして商を3/2と解答したりした児童がいたことが考えられます。
《これからの指導に向けて》
分数の意味については、その観点の置き方によって様々なとらえ方ができます。分数の意味の違いをとらえられるようにすることが大切です。
指導に当たっては、
| ・ |
商を小数まで割り進めても割り切れない場合があることを実際に計算して確認する活動を取り入れ、分数を用いることで商を1つの数として表せるというよさに気付くことができるようにすること。 |
| ・ |
求めた答えを確かめるような学習場面を設定し、答えを確かめることの大切さを理解させ、求めた答えを吟味する態度を育てること。 |
などが考えられます。
〔該当するプリント〕
分数と小数
|
|
| 設問ごとの分析結果とこれからの指導に向けて 【主として活用に関するB問題】 |
設問番号
1(2)
(数量関係)
正答率
39.2
無解答率
10.2
|
〔設問の概要〕…おつりを正しく求められるように式に( )を書き加える。
〔出題の趣旨〕…示された場面を解釈して、計算の順序についてのきまりを基に式を修正する。 |
〈分析結果と課題〉
この問題では、言葉の式の意味を理解して計算の順序を考え、正しい式を完成することが求められます。計算の順序についてのきまりを理解し、最初に考えた式に( )を書き加えて正しい式に修正することに課題があります。これは、かけ算に着目して「500−50+(150×2)」と
、150×2の部分に( )をかいた児童がいたことが考えられます。
《これからの指導に向けて》
( )を用いると、数量の関係をひとまとまりとして表すことができるというよさを理解できるようにすることが大切です。
指導に当たっては、
| ・ |
四則が混合したり、( )が用いられたりした計算が確実にできるようにすること。 |
| ・ |
複数の式(分解式)を総合式に表現し直す学習の場面を設定し、( )の用い方が正しいかどうかを確認したり、実際に計算をしてみて計算の順序についてのきまりを確認したりする活動を取り入れること。 |
などが考えられます。
〔該当するプリント〕計算のきまり |
設問番号
2(1)
(図形)
正答率
26.9
無解答率
11.8 |
〔設問の概要〕…本立ての部品の図を見て、どのような長方形かを書く。
〔出題の趣旨〕…示された図形を観察して、長方形の大きさを筋道を立てて考え、数学的に表現する。 |
〈分析結果と課題〉
この問題は、合同の意味や図形を表現する仕方を理解していることが求められます。平面上にかかれた立体図形や平面図形、与えられた条件を基に長方形の大きさを考え、それを辺の長さと言葉を用いて記述することに課題があります。これは、与えられた条件を基に長方形の辺の長さ15cm、20cmを求めることはできても、辺を表す言葉や形を表す言葉を用いて表現できていない児童がいたことが考えられます。
《これからの指導に向けて》
問題に示された数値や条件を基に、分かることを1つ1つ明らかにしていき、筋道を立てて考え、問題を解決できるようにすることが大切です。
指導に当たっては、
| ・ |
合同な図形を調べるときには、 等しい辺に印を付けるようにさせ、対応する辺の確認やその位置関係の確認をできるようにすること。 |
| ・ |
基本的な平面図形をかいたり作ったりする場面で、辺を表す言葉や長さ、角の大きさ、図形の名称を用いて、図形を言葉で表現し伝え合う活動を取り入れ、曖昧な表現でなく図形を的確に表現できるようにすること。 |
| ・ |
考え方を話し合う場面で、算数の用語を用いて図形を表現できているかなどを確認できるようにすること。 |
などが考えられます。
〔該当するプリント〕 合同な図形 「やってみようプリント」
|
設問番号
4
(量と測定)
(図形)
正答率
35.5
無解答率
19.0 |
〔設問の概要〕…平行四辺形から台形に図形を変えて、示された2つの三角形の面積が等しいことの
説明を書く。
〔出題の趣旨〕…示された説明を解釈し、用いられている考えを別の図形に適用して説明を考え、その
説明を数学的に表現することができる。 |
〈分析結果と課題〉
この問題は、平行四辺形に対してなされた説明が台形に適用できることを理解し、示された説明のどの部分をどう変えればよいかを考えることが求められます。平行四辺形に対してなされた説明を解釈し、それを台形に適用して、示された面積が等しいことの説明を言葉を用いて記述することに課題があります。これは、問題で示されている説明が解釈できなかった児童や、説明は解釈できていても、それを台形に適用できなかったり、表現の仕方が分からなかったりした児童などがいたと考えられます。
《これからの指導に向けて》
他者が記述した言葉の説明を解釈できるようにすることや根拠を明らかにして考えを進め、その考えを口述できるようにするとともに記述できるようにすることが大切です。
指導に当たっては 、
| ・ |
図形の性質などを根拠にして考えを進め、考えを言葉で説明できるようにすること。その際、根拠を含んで説明が記述されているかを確認したり、考えが友達に伝わるように記述されているかを確認したりさせること。 |
| ・ |
友達の言葉の説明を解釈できるようにするとともに、その考え方を用いて他の問題を解決させること。 |
| ・ |
説明の一部を提示しておいて残りの説明を完成する活動を取り入れるなど、児童の実態や授業のねらいに応じて活動の中身を工夫すること。 |
| ・ |
答えだけでなく解決過程に児童が着目できるようにすること。 |
などが考えられます。
〔該当するプリント〕四角形の面積 「やってみようプリント」
|
設問番号
5(2)
(数量関係)
正答率
16.1
無解答率
3.9 |
〔設問の概要〕…割引券を使うと値引きされる金額が最も大きくなる商品を選び、そのわけを書く。
〔出題の趣旨〕…割合が使われている場面を理解し、割合の考えを基に、数の大小を判断し、その
判断の理由を数学的に表現する。 |
〈分析結果と課題〉
この問題は、比較量、基準量、割合の関係を基に、比較量の大小を判断することが求められます。割合が一定の場面で、比較量が最も大きくなるときの基準量を判断し、その理由を言葉や式を用いて記述することに課題があります。これは、くつに割引券を使うと値引きされる金額が一番大きくなると判断できているものの、理由の記述が不十分であったり、誤りを含んでいたり、理由を書いていなかったりする児童がいたと考えられます。
《これからの指導に向けて》
判断の理由やある事柄が成り立つ理由を説明する際に、根拠となる事柄を明らかにして論理的に説明できるようにすることが大切です。
指導に当たっては、
| ・ |
(定価)×(割引率)=(値引きされる金額)
の数量の関係は同じであり、この式を根拠として言葉による説明が同じようにできることを確認して、言葉で説明することのよさに児童が気付くことができるようにすること。 |
| ・ |
説明の仕方を考える際に、児童の実態に応じて、定価が高いほど値引きされる金額が大きくなることを、図を基に理解できるようにしたり、実際の計算結果を基に理解できるようにしたりすること。 |
| ・ |
説明に必要な事柄を教師が分かりやすく板書して児童が理解できるようにしたり、ノートに整理して書かせる活動を取り入れたりすること。 |
などが考えられます。
〔該当するプリント〕くらべ方を考えよう(%) 「やってみようプリント」
|
設問番号
6(2)
(図形)
正答率
11.0
無解答率
8.4 |
〔設問の概要〕…バスのドアが動く様子を表した図を見て、円周の一部と直線の長さの大小について
の正しい記述を選び、判断のわけを書く。
〔出題の趣旨〕…日常の事象を数理的にとらえ、示された考えを基に、長さの求め方と長さの大小を
判断した理由を数学的に表現する。 |
〈分析結果と課題〉
この問題は、円周の求め方を理解していること、示された図や考えを基に、求める部分が円周の4分の1に当たると判断することが求められます。示された図や考えを基に、長さの大小を判断し、その判断の理由を円周の4分の1の長さを求める式と言葉を用いて記述することに課題があります。これは、「2」を選択しているものの、Bを示す言葉やBの長さを求める式を書いていなかったり、円周を(半径)×(半径)×(円周率)で求めていたりする児童がいたと考えられます。
《これからの指導に向けて》
式を書いて自分の考えや解決方法を説明する際に、なぜその式になるのかという根拠や、何を求めようとする式なのかという説明の対象を明らかにして説明できるようにすることが大切です。
指導に当たっては、
| ・ |
問題から分かることは何かを話し合う活動を取り入れ、半径(50cm)が分かるから円周の長さを求められるということに気付けるようにしたり、円周のどれだけに当たるかについて、角の大きさが90度であることに着目すればよいことに気付くことができるようにしたりすること。 |
| ・ |
児童の説明を基に、分かりやすく説明されている内容を確認したり説明を補わなければならない内容を話し合ったりする活動を取り入れること。 |
| ・ |
「何に着目すればよいか」、「問題から分かることは何か」、「習ったことの何が使えそうか」、などを話し合う活動を取り入れること。 |
などが考えられます。
〔該当するプリント〕 円周と円の面積 「やってみようプリント」
|
|
| 〈参考〉国立教育政策研究所Webページ http://www.nier.go.jp |
|
以上のように分析及び考察を行いました。
詳しい結果や指導のアイディアなどを知りたい方は下記のリンクを参照してください。 |
○調査結果の詳細は 〜佐賀県教育委員会Webページ
https://www.saga-ed.jp/kenkyu/scholastic_attainments_analysis/index.html
○平成22年度全国学力・学習状況調査結果を踏まえた実践アイディア集
〜国立教育政策研究所Webページ
http://www.nier.go.jp/10chousakekkahoukoku/10jugyourei.htm |