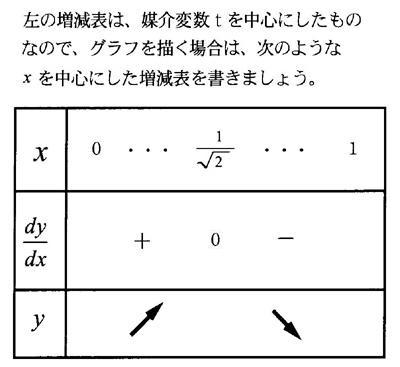
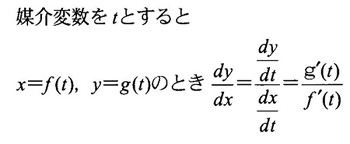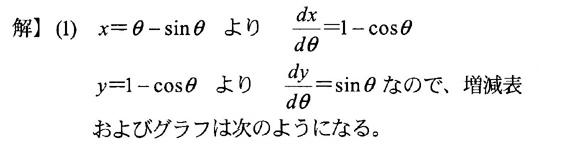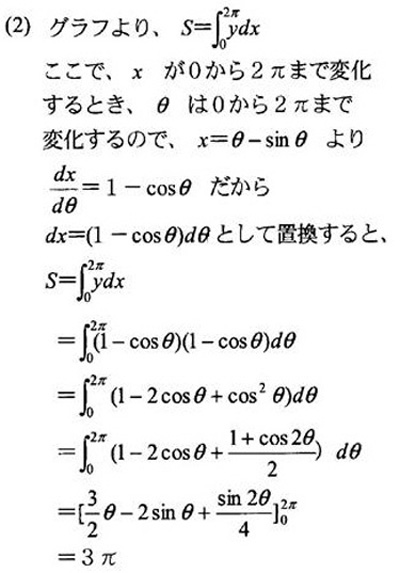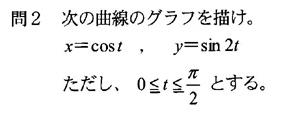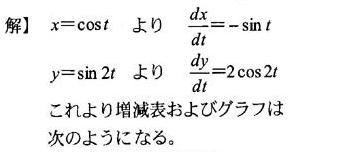数学Ⅲの教科書には、次のような媒介変数で表示された関数の導関数の公式があります。
そして、この公式を用いる代表的な例題として、次のようなものがあります。
しかし、この例題は単なる計算に終始し、関数のグラフのイメージが欠落していると思われます。
媒介変数表示のままでは、関数のグラフの概形が分かりにくく、関数のイメージがつかみにくい
のではないでしょうか。
このとき、通常は、次のように媒介変数を消去することを指導します。
①は2次関数なのでグラフが容易に描け、生徒は媒介変数表示で与えられた関数のイメージが出来るでしょう。
先生方は、この段階で、円や楕円の媒介変数表示から媒介変数を消去することも補足されることと思います。
媒介変数が容易に消去でき、グラフの概形もすぐに求まる場合、この方法は有力です。
しかし、媒介変数を消去することが厄介な問題や、消去しても関数のグラフの概形が分かりにくい問題も
少なくありません。
そこで、ほとんどの教科書には掲載されていませんが、媒介変数を消去しない関数のグラフの
描き方を指導する必要があると思います。
それには、次の問1(サイクロイド)や問2(リサジュ曲線)などを例に挙げて指導されてみては
いかがでしょう。
生徒たちは、媒介変数表示が抵抗なく受け入れられるようになると思います。
| 媒介変数を消去せずに関数のグラフを描く問題例(サイクロイド) |
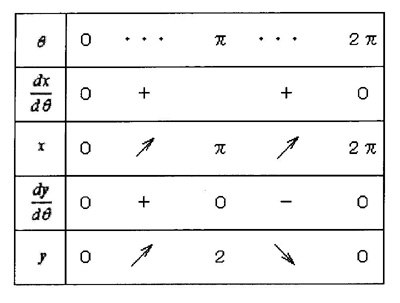
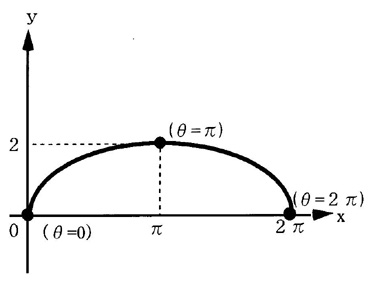
| 【考え方】 媒介変数で表示された関数のグラフを描く |
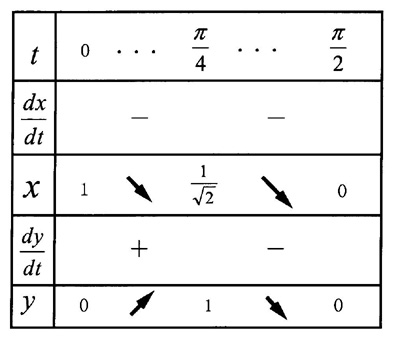
| 媒介変数を消去せずに関数のグラフを描く問題例(リサジュ曲線) |
|