※ 部分積分法を利用した定積分では、次の3つの問題点があると思われます。
(1)定積分内の2つの被積分関数のどちらを微分し、どちらを積分すべきなのかが分かりにくい。
(2)計算の途中で符号が変化することが多く、計算ミスを起こしやすい。
(3)部分積分を何回行えば定積分が求まるのか、見通しがつきにくい。
そこで、微分法の線形性を利用した積分法を紹介します。この積分法は、
◎ 見通しがつき、分かりやすい
◎ 2回の積分が不要である
の利点があり、部分積分法の3つの問題点(1)~(3)を解消できます。
まずは、次の例をご覧ください。
 |
この例の結果は準公式のようなものですが、次の例題のような問題を何問か演習すれば、
この積分方法が定着するものと思われます。
続いて【解法1】(微分法の線形性を利用した解法)と【解法2】(通常の部分積分法による解法)
を紹介します。【解法1】では【解法2】の部分積分に伴う符号の変化がありませんので、計算ミスによる
間違いをよくしてしまう生徒には、特にお勧めです。
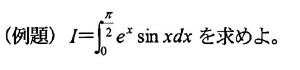 |
| 【考え方】 |
 |
| 【解法1】(微分法の線形性を利用した解法) |
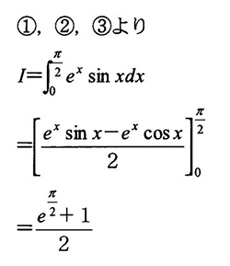 |
| 【解法2】(通常の部分積分法による解法) |
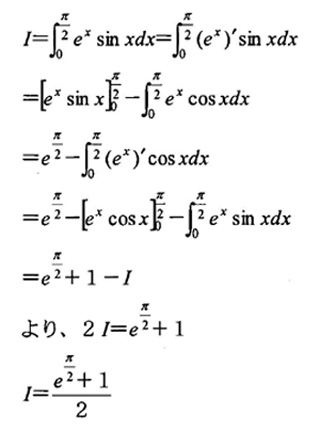 |
 |
 |