|
|
|
|
��b�E��{
�����w�I�Ȍ�����l���� |
�܂����₷���_�̗� |
�w���̃|�C���g |
|
|
|
|
|
|
|
| �� |
�����C�O�p�`�C�l�p�`�̗����B |
| �� |
�O�p�`�C�l�p�`���������������肷�� |
| �� |
�����̐��ŎO�p�`�C�l�p�`���������B |
|
| �E |
�����̈Ӗ��̗������\���łȂ��B |
| �E |
�_�Ɠ_�����܂����ׂȂ��B |
| �E |
�����������Ȃ��B |
|
| �� |
�|�Ђ���W�I�{�[�h�ŎO�p�`��l�p�`������̕�����̊�����������C�����ň͂܂ꂽ�}�`�ł��邱�Ƃ��ӎ�������B |
| �� |
�����ƋȐ����r�����C�Ⴂ������������B |
| �� |
�h�b�g�}�ŁC���т����Q�_�Ɉ��t���C��K��p���Ē���������������������B |
| �� |
��K�̒u�������w�����C���ᎆ�Œ�K���g���Ē������������K��������C��}�Ɋ��ꂳ����B |
|
|
|
|
|
| ���w�R�N |
�����`��
�����` |
| ���p�O�p�` |
|
| �� |
�����`�C�����`�C���p�O�p�`�C���p�C�ӁC���_�̗����B |
| �� |
�����`�C�����`�C���p�O�p�`����}������A������肷��B |
| �� |
�~���l�ߖ͗l������B |
| �� |
�ӂ̒����Ⓖ�p�ɒ��ڂ��āC�����`�C�����`�C���p�O�p�`�̐������l����B |
|
| �E |
�}�`�̈Ӗ�����p��ӂ̒����Ȃǂ̗p���p���Đ����ł��Ȃ��B |
| �E |
��}���ł��Ȃ��B |
|
| �� |
�}�`���r�����C�ӂ̒����Ⓖ�p�Ȃǂɂ��Č������銈�����������B |
| �� |
���p��ӂɈ��t�������C�p��ƑΉ������Ȃ���J��Ԃ�����������B�y�W�J��P�i���j��.14�`16�z |
| �� |
������傫����ς����}�`�i�����`�j���r�������銈����ʂ��āC��`����������B |
| �� |
�h�b�g�}��p���C���_���ӎ����Ē����`�C���O�p�`�C���p�O�p�`����}������B
���̌�C���ᎆ�ł̍�}���������B�@ |
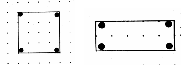 |
| �i�h�b�g�}��p������}�j |
|
|
|
|
|
|
|
| �� |
�~�C���S�C���a�C���a�̗����B |
| �� |
�R���p�X���g���ĉ~����}������C������肷��B |
| �� |
���슈����ʂ��āC�~�̐������l����B |
|
| �E |
���a�C���a�̗������\���łȂ��B |
| �E |
�R���p�X�����܂��g���Ȃ��B |
|
| �� |
�~�ɔ��a�Ⓖ�a����������銈����ʂ��āC�����������邱�Ƃ�����������B�܂��C���������ׂē����ł��邱�Ƃ��C���ۂɑ��邱�ƂŊm���߂�����B |
| �� |
�R���p�X�̐j�������Ȃ��悤�Ɍ�����~���C�������ɗ��ӂ����C�~����������B |
| �� |
�~��g�ݍ��킹���͗l���┼�a�̒����𑪂��銈���𑽂�������C�R���p�X���g������}�Ɋ��ꂳ����B |
|
| ���w�S�N |
| �ӎO�p�` |
| ���O�p�` |
|
| �� |
�ӎO�p�`�C���O�p�`�C�p�̗����B |
| �� |
�ӎO�p�`�C���O�p�`���C�R���p�X���g���č�}������C������肷��B |
| �� |
�~���l�ߖ͗l������B |
| �� |
�ӂ̒�����p�ɒ��ڂ��āC�ӎO�p�`�C���O�p�`�̐������l����B |
|
| �E |
�ӂ̒�����p�̑傫���̑������m���߂���@���v���t���Ȃ��B |
| �E |
�}�`�̈Ӗ������ӂ̒�����p�̑傫���Ȃǂ̗p���p���Đ����ł��Ȃ��B |
|
| �� |
������Đ}�`�����C�܂�Ȃ�����d�˂��肵�āC�ӂ̒�����p�̑傫�����m���߂�Ƃ����������J��Ԃ��������B |
| �� |
��̓I���슈���𐔑���������C�}�`�̐����ɂ��ċC�t�������Ƃ���������������������肷��B |
| �� |
�}�`�̍\���v�f�i�p��j���g���āC�}�`�̈Ӗ����܂Ƃ߂���C�}�`�̐���������������肷��B |
|
|
|
| �� |
�p�x�̒P�ʂƑ���̈Ӗ��̗����B |
| �� |
���x����g���Ċp�̑傫���𑪒肷��B |
| �� |
���O�p�`��ӎO�p�`�C�O�p��K�̊p�̑傫����m��B |
| �� |
�p�̑傫������]�̑傫���Ƃ��C�ʓI�ɂƂ炦�邱�Ƃ��ł���B |
| �� |
����p�x���Q�̊p�̘a�ƍ��Ƃ݂�Ȃǂ��āC����̎d���₩�������l����B |
|
| �E |
�p�̑傫���̗ʊ����\���ɂ��߂Ă��Ȃ��B |
| �E |
���x�킪���܂��g���Ȃ��B |
|
| �� |
����g���āC���悻�̊p�����銈����������C�p�̑傫���ɂ��Ă̊��o����Ă�B |
| �� |
�p�x�𑪂�O�ɁC���p�i90���j���傫�����ǂ���������t��������B |
| �� |
�ǂ̊p�𑪂�̂��ӎ������邽�߂ɁC���t������C�C���X�g�𗘗p������ ����B |
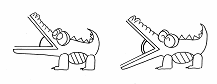 |
| �i�C���X�g�ŕ\�����p�x�𑪂���j |
| �� |
�͗l���Ȃǂ̑��슈����������C�V�т�ʂ��Ċp�̑�����̎w��������B�@�@�@ |
|
|
|
|
|
|
|
| �� |
�~�����̈Ӗ��Ɖ~�������߂�����̗����B |
| �� |
�������g���ĉ~���Ⓖ�a�����߂�B |
| �� |
�~�̒��a�Ɖ~���̊W���l����B |
|
| �E |
�~�̉~�������߂�����𗝉����Ă��Ȃ��B |
| �E |
�����̓K�p���i�����}�`�j���ł��Ȃ��B |
|
| �� |
�~�i���^�j�̒��a�𑪂�C�����]�����ĉ~���𑪂銈����ʂ��āC�~�������߂�������w�K���������i��������~�������j�B |
| �� |
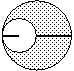
�R���p�X�Ŗ͗l�����������Ƃ�z�N�����C�����}�`�̂ǂ��ɔ��a�Ⓖ�a�����邩�C���t���������蒼�������������肷��B |
|
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����}�`�̖��j |
|
|
|
|
|
|
|
| �� |
�����C���s�̊W�̗����B |
| �� |
�O�p��K���g���āC�����╽�s�̊W�ɂ��钼������}����B |
| �� |
�����̌������ɒ��ڂ��āC�����E���s�̊W���l����B |
|
| �E |
�Q�̒����̐����C���s�̊W�̗������\���ł͂Ȃ��B |
| �E |
���s�Ȑ��␂���Ȑ������܂������Ȃ��B |
|
| �� |
�����E���s�̈ʒu�W���C�_�Ȃǂ̋�̕����g���Ď��o�I�ɂƂ炦������B |
| �� |
���̂悤�ȃX�e�b�v�Ŏw������i�@���ᎆ���g������}�@�A��{�̒������g������}�@�B�Q�̎O�p��K��p������}�j�B |
|
|
|
|
|
| ���w�T�N |
| ��` |
| ���s�l�ӌ` |
| �Ђ��` |
| ���p�` |
|
| �� |
���s�l�ӌ`�C��`�C�Ђ��`�̗����B |
| �� |
���s�l�ӌ`�C��`�C�Ђ��`����}����B |
| �� |
�~���l�ߖ͗l������B |
| �� |
�ӂ̈ʒu�W�i�����E���s�j�ɒ��ڂ��āC���s�l�ӌ`�C��`�C�Ђ��`�̐������l����B |
|
| �E |
�}�`�̈Ӗ������ӂ̕��s�E�����Ȃǂ̗p���p���Đ����ł��Ȃ��B |
| �E |
��}���\���ɂł��Ȃ��B |
|
| �� |
��̓I���슈���𐔑���������C�}�`�̐����ɂ��ċC�t�������Ƃ���������������������肷��B |
| �� |
�}�`�̍\���v�f�i�p��j���g���āC�}�`�̈Ӗ����܂Ƃ߂��萫��������������肷��B |
| �� |
���s�����g���č�}������C���ᎆ�̂܂��ڂ��g���č�}�����肷��ȂǁC�i�K��݂��āC�}�`�̐������m�F���Ȃ���w������B |
|
| �� |
�O�p�`�̓��p�̘a�@180���̗����B�l�p�`�̓��p�̘a�@360���̗����B |
| �� |
���슈����ʂ��āC�O�p�`��l�p�`�̊p�̑傫���ɂ��čl����B |
|
| �E |
�O�p�`�̓��p�̘a��K�p������ŁC�O�p�`�̓��p��O�p�����߂邱�Ƃ��ł��Ȃ��B |
| �E |
���p�`�̊p�̘a�����߂���@���l�����Ȃ��B |
|
| �� |
���߂�p�ɉ������������ĊO�p���Ƃ炦��������C�p�̑傫���Ɍ�����t���������肵�āC�p�x�̌������L����B |
| �� |
�����`����`���O�p�`�ɕ����銈����z�N�����C���p�`�ɕ⏕�������邱�ƂŐ}�����Č��邱�ƂɋC�t������B |
|
|