�ߒ� |
|
�w����̗��ӓ_�i���j�A�]���K���ƕ]�����@�i���j
�Z���I�����i���j |
|
���� |
| �P |
�@�{���̖���m��A�ۑ���Ƃ炦��B |
| |
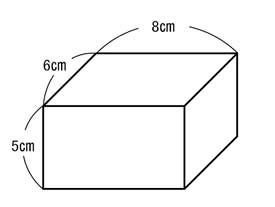
��}�@�v���[���g�̔��� |
| |
 |
�@ |
| �� |
��蕶�����ۂɂ́A�v���[���g�̔��̐}�������Ȃ���������邱�ƂŁA��ӂ��Ƃ炦�₷������B |
|
�k���P�l
�Ȃ�������́A�Ƃ̐l�Ƀv���[���g�������낤�Ǝv���Ă��܂��B�}�̂悤�Ȕ��̒��Ƀv���[���g�����Ă킽�����Ǝv���Ă���̂ł����A���̂܂��������ł����肽���Ǝv���܂����B�����ŁA�F���̂��ׂĂ̖ʂɂ͂��Ă����낤�ƍl���܂����B�ނ��Ȃ��p�ӂ���ɂ́A�����u�̐F��������悢�ł��傤�B |
|
| �� |
���K������U��Ԃ�A�ʐς̌������g���ċ��߂��邱�ƂɋC�t�����A�ۑ���Ƃ炦������B |
|
| ���̌`���悭���āA�ʐς����߂悤�B |
|
| ���ʂ� |
| �Q |
�@�����̔����ώ@���邱�Ƃ�ʂ��āA�����̌��ʂ������B |
| ���\�z����鎙���̍l���� |
| |
�E |
�e�ʂ̒����`�̖ʐς����߂Ă����B |
| |
�E |
�����`�̓����ʂ��Q�����邱�Ƃ𗘗p���Ėʐς����߂�B |
|
| �� |
�O���[�v�ɂP������p�ӂ���B |
| �� |
�����̔����ώ@���邱�ƂŁA���̖ʂ͂U�̒����`�ō\������Ă��邱�Ƃ�A�����������ʂ̑傫���������ł��邱�ƂȂǂɂ��āA�C�t������B |
|
| ���͉��� |
| |
�E |
�u�v���[���g�̔��̐}�v���璷���`�̕ӂ̒������l������A���̖ʂ��ʂ�������肷��Ȃǂ��āA�ʐς����߂鎮��l�����������B |
|
| �� |
���ۂɔ����ώ@�������Ƃ�}�����čl�������Ƃ����ɕ\������B�܂��A�}�⎮���Ƃ炵���킹�čl�������Ƃ��A�F�����ɕ�����₷�������ł���悤�ɁA�m�[�g�ɋL������A���t�Ȃǂ���ꂳ����B(�) |
|
�w�э��� |
| �S |
�@�����̍l�����y�A�Ő����������B |
| |
�E |
�p���������Ȃ���A�����̍l�����������B |
| |
�E |
�����̍l���Ǝ��Ă���Ƃ���A�Ⴄ�Ƃ���A�F�B�̍l���̂悢�Ƃ���A������₷���Ƃ���ɋC�t���A���ꂼ��̍l���ɂ��ė�������B |
|
| �� |
���Ɣ��Ƃ�Ή������Ȃ���A����ӎ����������Đ���������B(�) |
| �� |
����̐������Ƃ��ɂ́A�����̍l���Ɠ������Ⴄ�����ӎ�������B�܂��A�悭������Ȃ��Ƃ���́A���݂��Ɏ��₵�����悤�ɂ�����B |
�@ |
|
�s�\�z����鎙���̍l���t |
| |
�E |
�e�ʂ̖ʐς����߂Ă����B |
| |
�E |
�����ʂ��Q������̂łQ�{���Ă����B |
| |
�E |
�ǂ̖ʂ��Q�ʂ�����̂ł܂Ƃ߂ĂQ�{����B |
| |
|
|
|
| �� |
�������\�����A�ǂ̂悤�ɍl�������𑼂̎����ɐ���������B(�) |
| �� |
�Q�������`������A���ꂼ��Q�{���邱�Ƃ��A�S�̂̊w�э����̒��Ŋm�F����B |
| �� |
�ʐς̋��ߕ����ӂ�Ԃ�A�����̍l���ȊO�̕��@�����邱�ƂɋC�t���A���̉������𗝉�������B |
|
| �U |
�@�����p�b�N�ō������������̖ʂ̖ʐς����߂�B |
| |
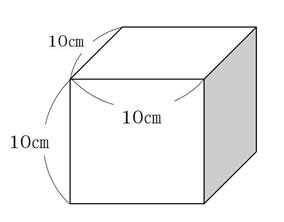
�s��������̐}�t |
| |
 |
|
| �� |
��蕶�����ۂɂ́A��������̐}�������Ȃ���������邱�ƂŁA��ӂ��Ƃ炦�₷������B |
| |
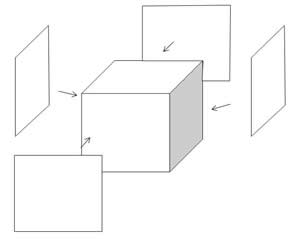
�፶�E�ƑO��̖ʂɐF�����͂�� |
| |
 |
|
�k���Q�l
�Ȃ�������́A�����p�b�N�ŏ����������肽���Ǝv���Ă��܂��B�}�̂悤�ȏ�������̍��E�ƑO��̖ʂɐF�����͂��Ă����낤�Ǝv���Ă��܂��B��������̖ʂ�1�ӂ̒����́A�P�O��m�ł��B�ނ��Ȃ��p�ӂ���ɂ́A�����u�̐F��������悢�ł��傤�B |
| |
�s�\�z����鎙���̍l���t |
| |
�E |
�e�ʂ̖ʐς����߂Ă����B |
| |
�E |
�����ʂ��S����̂łS�{����B |
|
| �� |
���ׂ������̖ʂ͓��������`�ł��邱�Ƃ�A4�̖ʂ̑傫���������ł��邱�Ƃɂ��āA��������̐}����C�t�����Ƃ��ł���悤�ɂ���B |
�@�@
���@���̖ʂ̍\�����l���A�����`����`�̖ʐς̌������g���Ĕ��̕\�ʂ̖ʐς����߂邱�Ƃ��ł���B
�y���w�I�ȍl�����z�m�ώ@�E�m�[�g�n
|
|
��
�Ƃ߂� |
| �V |
�@�{���̊w�K���܂Ƃ߂�B |
| ���܂Ƃ߁� |
| |
�E |
���̎���̖ʂ̖ʐς́A�����`����`�̖ʐς̌������g���ċ��߂�B |
| |
�E |
�����ʂ�����ꍇ�́A�܂Ƃ߂ċ��߂邱�Ƃ��ł���B |
| |
|
| �W |
�@�Z�����L�������B |
| �����������ۂɏ������Z�����L�̗၄ |
 |
| �� |
���̖ʂ̖ʐς́A���K�ł��钷���`����`�̖ʐς̌������g���ċ��߂��邱�Ƃɂ��Ă܂Ƃ߂�����B |
| |
|
| |
|
| |
|
| |
|
| |
|
| �� |
���̖ʂ̖ʐςׂ����Ƃɂ��Ċ��z����������B |
| |
|
|



