‰ك’ِ |
|
ژw“±ڈم‚ج—¯ˆس“_پiپ›پjپA•]‰؟‹Kڈ€‚ئ•]‰؟•û–@پiپپj
ژZگ”“Iٹˆ“®پiپپj |
‚آ‚©‚ق |
‚P |
–{ژ‚ج–â‘è‚ً’m‚èپA‰غ‘è‚ً‚ئ‚炦‚éپB |
[–â‘è]
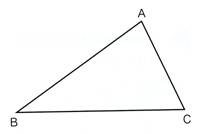
‰؛‚جژOٹpŒ`‚`‚a‚b‚ً‚Q”{‚ةٹg‘ه‚µ‚½ژOٹpŒ`‚c‚d‚e‚ج‚©‚«•û‚ًچl‚¦‚ـ‚µ‚ه‚¤پB
 |
|
| پ› |
‘Oژ‚جٹwڈK‚ًگU‚è•ش‚èپA–{ژ‚إ‚ح•ûٹل‚ج‚ـ‚·–ع‚ھ‚ب‚¢‚±‚ئ‚ًٹm”F‚·‚éپB |
|
| ژOٹpŒ`‚جٹg‘هگ}‚ج‚©‚«•û‚ًچl‚¦‚و‚¤پB |
|
| Œ©’ت‚· |
| ‚Q |
‰ًŒˆ‚جŒ©’ت‚µ‚ً‚à‚آپB |
| |
ژOٹpŒ`‚جٹg‘هگ}‚ً‚©‚‚½‚ك‚ة•K—v‚بڈî•ٌ‚ًچl‚¦‚éپB |
|
| پ› |
‚±‚ج‚ـ‚ـ‚إ‚حچىگ}‚إ‚«‚ب‚¢‚±‚ئ‚©‚çپAژOٹpŒ`‚ج‚ا‚ج•س‚ج’·‚³‚âپAٹp“x‚ھ’m‚肽‚¢‚©‚ً–₤پB |
| پ› |
‚±‚ê‚ـ‚إ‚جٹwڈK‚ًگU‚è•ش‚èپAٹùڈK‚جچ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚ھژg‚¦‚邱‚ئ‚ة‹C•t‚©‚¹‚éپB |
| پ› |
چ‡“¯‚بژOٹpŒ`‚ً‚©‚چغ‚حپA‚R‚آ‚جڈî•ٌ‚ھ•K—v‚¾‚ء‚½‚±‚ئ‚ًٹm”F‚·‚éپB |
| پ› |
چإڈ‰‚ح•س‚d‚e‚©‚ç‚©‚«ژn‚ك‚邱‚ئ‚ًٹm”F‚·‚éپB |
|
| ژ©—ح‰ًŒˆ |
| ‚R |
ژ©—ح‰ًŒˆ‚ً‚·‚éپB |
| |
ژOٹpŒ`‚جٹg‘هگ}‚ً‚©‚«پA‚»‚جچغ‚جچىگ}‚µ‚½ژèڈ‡‚âٹùڈKژ–چ€‚ج‰½‚ًژg‚ء‚½‚©‚ًƒmپ[ƒg‚ةڈ‘‚پB |
| |
پs—\‘z‚³‚ê‚éژ™“¶‚جچl‚¦پt
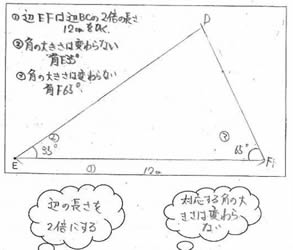
‡@•س‚`‚a‚ئ•س‚`‚b‚ج’·‚³‚ً‚»‚ꂼ‚ê‚Q”{‚ة‚µ‚ؤƒRƒ“ƒpƒX‚ًژg‚ء‚ؤٹg‘هگ}‚ً‚©‚پB
‡A•س‚`‚a‚ج’·‚³‚ً‚Q”{‚ة‚µ‚ؤپCٹp‚a‚ج‘ه‚«‚³‚ح‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤٹg‘هگ}‚ً‚©‚پB
‡Bٹp‚a‚ئٹp‚b‚ً‚»‚ج‚ـ‚ـ‚ة‚µ‚ؤ•ھ“xٹي‚ًژg‚ء‚ؤپAٹg‘هگ}‚ً‚©‚پB
|
پsژ™“¶‚ھژہچغ‚ةƒmپ[ƒg‚ة‚©‚¢‚½چl‚¦پt
 |
| پ |
چىگ}‚µ‚½‚à‚ج‚ة‚حژ©•ھ‚ھ’²‚ׂ½•س‚ج’·‚³پAٹp‚ج‘ه‚«‚³‚¾‚¯‚ًڈ‘‚«چ‚ـ‚¹‚éپBپiƒAپj |
| پ |
چىگ}‚µ‚½ژèڈ‡‚ھ•ھ‚©‚é‚و‚¤‚ةپAچىگ}‚µ‚½گ}Œ`‚ة”شچ†‚ً‹L“ü‚³‚¹‚éپB پiƒAپj |
| پ |
•¶ڈح‚إژèڈ‡‚ًڈ‘‚چغ‚ة‚حپA•ھ‚©‚è‚â‚·‚¢‚و‚¤‚ة‰سڈًڈ‘‚«‚ة‚³‚¹‚éپB پiƒAپjپ@ |
| پ |
ƒmپ[ƒg‚جگپ‚«ڈo‚µ‚ةپA‚ا‚ج‚و‚¤‚بٹùڈKژ–چ€‚ًژg‚ء‚½‚©‚ًڈ‘‚©‚¹‚éپBپiچ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚âپAٹg‘هگ}پEڈkگ}‚جگ«ژ؟پj پiƒAپj |
| پ› |
“§–¾ƒVپ[ƒg‚ةژOٹpŒ`‚`‚a‚b‚ً‚Q”{‚ةٹg‘ه‚µ‚½ژOٹpŒ`‚c‚d‚e‚ًˆَچü‚µ‚½‚à‚ج‚ً—pˆس‚µ‚ؤ‚¨‚«پCچىگ}‚µ‚½گ}Œ`‚ئڈd‚ثچ‡‚ي‚¹‚³‚¹ٹشˆل‚ء‚ؤ‚¢‚ب‚¢‚©‚ًٹm‚©‚ك‚³‚¹‚éپBپ@ |
|
| ٹw‚رچ‡‚¢ |
‚S |
ژ©•ھ‚جچl‚¦‚ًƒOƒ‹پ[ƒv‚إ‚¨Œف‚¢‚ةگà–¾‚µچ‡‚¤پB |
|
پE |
چىگ}‚µ‚½گ}Œ`‚âپAڈ‘‚«چ‚ٌ‚¾‚±‚ئ‚ًٹî‚ةژèڈ‡‚ًگà–¾‚·‚éپB |

پuژèڈ‡‚ًژ¦‚µ‚ب‚ھ‚çگà–¾‚µ‚ ‚ء‚ؤ‚¢‚é—lژqپv |
| پ |
چىگ}‚جژèڈ‡‚ھ•ھ‚©‚é‚و‚¤‚ةپu‚ـ‚¸پAژں‚ةپcپv‚ئ‚¢‚ء‚½ڈ‡ڈک‚ً•\‚·Œ¾—t‚ًژg‚ء‚ؤگà–¾‚³‚¹‚éپBپiƒCپj |
| پ› |
‚ا‚ج‚و‚¤‚بٹùڈKژ–چ€‚ًٹˆ—p‚µ‚ؤ‚¢‚é‚ج‚©‚ًˆسژ¯‚µ‚ؤ•·‚©‚¹‚éپB |
|
‚T |
چl‚¦‚½‚±‚ئ‚ًƒOƒ‹پ[ƒv‚ج‘م•\‚ھ”•\‚µپA‘S‘ج‚إکb‚µچ‡‚¤پB |
| |
پu‘S‘ج‚جڈê‚إگà–¾‚µ‚ؤ‚¢‚é—lژqپv |
|
| پ› |
ٹg‘هگ}‚ج‚©‚«•û‚ة‚آ‚¢‚ؤپAژO’ت‚è‚ج•û–@‚ًگà–¾‚³‚¹‚éپB |
| پ› |
ٹùڈKژ–چ€‚ج‰½‚ًژg‚ء‚½‚©‚ً–â‚¢پAچ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚âٹg‘هگ}‚جگ«ژ؟‚ًٹˆ—p‚µ‚ؤ‚¢‚邱‚ئ‚ًٹm”F‚·‚éپB |
|
| ‚ـ‚ئ‚ك‚é |
‚U |
–{ژ‚جٹwڈK‚ً‚ـ‚ئ‚ك‚éپB |
|
پ@چ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚ًژg‚¤‚ئٹg‘هگ}‚ً‚©‚‚±‚ئ‚ھ‚إ‚«‚éپB |
[–â‘è]
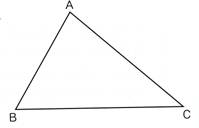
ژOٹpŒ`‚`‚a‚b‚ج
‡@‚P/‚Q‚جڈkگ}‚ً‚©‚«‚ـ‚µ‚ه‚¤پB
‡A‚Q”{‚جٹg‘هگ}‚ً‚©‚«‚ـ‚µ‚ه‚¤پB
 |
‚W |
–{ژ‚جٹwڈK‚ًژZگ”“ْ‹L‚ة‚ـ‚ئ‚ك‚éپB |
| |
پsژ™“¶‚ھژہچغ‚ةڈ‘‚¢‚½ژZگ”“ْ‹L‚ج—لپt |

|
| پ› |
ژOٹpŒ`‚جٹg‘هگ}پAڈkگ}‚ً‚©‚چغ‚ة‚حپAٹg‘هگ}پAڈkگ}‚جگ«ژ؟‚âچ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚ًژg‚¦‚خ‚©‚¯‚邱‚ئ‚ً‚ـ‚ئ‚ك‚éپB |
| پ› |
‚P/‚Q‚جڈkگ}‚ً‚©‚‚±‚ئ‚ھ‚إ‚«‚½ژ™“¶‚ة‚حپA‚Q”{‚جٹg‘هگ}‚ً‚©‚‚و‚¤‚ة’m‚点‚éپB |
| پ› |
ژ©—ح‰ًŒˆ‚ج‚ئ‚«‚ةٹˆ“®‚ھ’â‘ط‚µ‚ؤ‚¢‚½ژ™“¶‚ة‚حپA•س‚a‚b‚ً‚P/‚Q‚ة‚µ‚ؤپAژں‚ة‚ا‚جڈî•ٌ‚ھ•K—v‚©‚ً”آڈ‘‚ًژQچl‚ة‚³‚¹‚ؤژو‚è‘g‚ـ‚¹‚éپB |
پ چ‡“¯‚بژOٹpŒ`‚ج‚©‚«•û‚ًٹî‚ةپAژOٹpŒ`‚جٹg‘هگ}پAڈkگ}‚ج‚©‚«•û‚ًچl‚¦‚ؤ‚¢‚éپB
پyگ”ٹw“I‚بچl‚¦•ûپz[ƒmپ[ƒgپAٹدژ@] |
| پ› |
ژِ‹ئ‚إ•ھ‚©‚ء‚½‚±‚ئ‚âٹ´‘zپA‚±‚ê‚©‚ç‹C‚ً‚آ‚¯‚½‚¢‚±‚ئ‚₳‚ç‚ة’²‚ׂؤ‚ف‚½‚¢‚±‚ئ‚ب‚ا‚ًڈ‘‚©‚¹‚é‚و‚¤‚ة‚·‚éپB |
|





