過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
つかむ |
[問題]
下の三角形ABCで、(頂点Bとほかの頂点A、Cを結ぶ直線を)利用して2倍の三角形GBHをかきましょう。
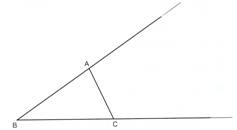 |
|
| ○ |
既習事項を振り返り、三角形の拡大図のかき方を確認する。 |
| ○ |
一つの点と他の頂点を結ぶ際、基になる点を「中心」とよぶことを知らせる。
|
|
|
|
| 見通す |
| 2 |
解決の見通しをもつ。 |
| |
《予想される児童の考え》
・2辺とその間の角の大きさに着目する。
・1辺とその両はしの角の大きさに着目する。 |
|
| ○ |
どんな道具が必要かを話し合い、コンパスも使えることを確認する。 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
| |
《予想される児童の考え》
・辺AB、BCの2倍の長さの所の点をそれぞれ頂点G、Hにする。
・辺ABの2倍の所に頂点Gを取る。角Gを80°にして辺BCを伸ばした直線と交わった点を頂点Hにする。
・辺BCの2倍の所に頂点Hを取る。角Hを65°にして辺BAを伸ばした直線と交わった点を頂点Gにする。 |
|
| ◎ |
一つの点を中心にして、拡大図をかかせる。 (ア) |
| ○ |
作図の際に使ったコンパスのあとなどは残しておくように伝える。 |
| ○ |
2倍に拡大した図をかいた透明シートを準備しておき、できた児童が確認できるようにしておく。 |
◇ 一つの点を中心にした三角形の拡大図、縮図のかき方を考えている。
【数学的な考え方】[ノート、行動観察] |
| ○ |
活動が停滞している児童には、1つの点を中心にした拡大図の作図のしかたを振り返らせる。 |
|
| 学び合い |
|
| ◎ |
一つの点を中心にした拡大図のかき方を説明させる。(イ) |
| ○ |
作図した図形をもとに説明させ、かき方が間違っていないかもお互いに確かめさせる。 |
|
5 |
考えたことをグループの代表が発表し、全体で話し合う。 |
| 《発表した児童の考え》 |
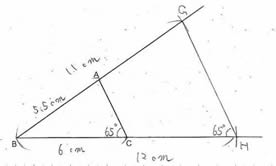

|
| ○ |
一つの点を中心にした三角形の拡大図の作図にも、既習の拡大図・縮図の性質を活用していることを確認する。 |
※児童がかいている「2辺1角」とは、拡大図をかくときに2つの辺とその間の角を調べればかくことができる、ということを示している。
|
| まとめる |
[問題]
下の四角形ABCDの2倍の拡大図をかきましょう。
 |
| 8 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際にノートにかいた算数日記》 |

|
| ○ |
拡大図のかき方を活用すれば、一つの点を中心にして拡大図をかくことができることを確認する。 |
| ○ |
四角形の拡大図もかくことができないかを問い、対角線を上手に使えば、作図することができそうであることを知らせる。 |
| ○ |
四角形には角の大きさが示されていないことを確認し、辺の長さや対角線の長さを使っていくことを確認する。 |
| ○ |
授業で分かったことや感想、これから気をつけたいことやさらに調べてみたいことなどを書かせるようにする。 |
|




