過程 |
学習活動
算数的活動 |
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動の指導にかかわる留意点(◎) |
つかむ
|
1 本時の課題をとらえる。
・本時の学習問題を把握する。
・本時の学習問題に対する自分の考えを発表する。
|
○下の図のようなティッシュの箱(直方体)と2つの面の関係が平行になっていない箱を用意することで、面と面の関係の違いに関心をもたせる。 ( 2つの面の関係が平行になっていない箱の展開図)
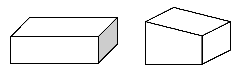
◎直感的に分かる程度のことを、具体物を見たり操作したりすることで理解させ、考えを発表させる。
◇直方体がいつもきちんと積み重ねられる理由を考えようとしている。
【興味・関心・態度】
〔発表・行動観察〕
|
○ティッシュの箱が直方体になっていることを確認させる。
○2つの面の関係が平行になっていない箱では、いつもはきちんと積みあがらないことを認識させ、いつもきちんと積み重なる直方体の特徴に目を向けさせる。 |
2 めあてを確かめる。
|
|
| ティッシュの箱が積み重なりやすいひみつをさがそう。 |
|
| |
○ティッシュの箱を直方体と確認させ、直方体の構成要素や面の関係について学習することを意識させる。 |
見通す
|
3 見通しをもつ
≪自力解決のための見通し≫
・「面の形」(長方形)
|
|
○面と面との関係に、まず目を向けさせる。
○既習事項の辺と辺との関係について、掲示しておき、見通しの手立てとする。
<掲示しておく関係図> (三角定規の活用を示す。)
・辺と辺との平行の関係
・辺と辺との垂直の関係
|
|
自力解決
|
4 直方体が重なりやすいひみつを調べる。
(予想される考え)
・向かい合っている面が平行
・底の面と立っている面が垂直
・・・・・・
|
|
◎直方体を使って、面と面との関係を見付けさせる。
○掲示しておいた辺と辺との関係に着目して直方体の面について考えるように注意を促す。
○考えをかき終えた児童には、いつもきちんと積み重なる理由となっているのか、また、他の理由はないかを考えさせる。 |
学び合い |
5 自分の考えを説明する。
・考えについて、グループで話し合う。 |
◎いつもきちんと積み重ねることができる理由となっているのか、出された考えを順に検討し、賛否と理由をワークシートに書かせる。 |
6 全体の場で説明し合う。

「説明を補助する児童」
|
○全体での話し合いでは、理由を検討しながら、直方体の面と面との関係について確認させる。
「操作を交えて発表する児童」
|
・向かい合っている面は平行である → 平行でないと落ちてしまう。
(何組あるのかを確かめさせる。) → 3組
・隣り合う面は垂直な面である。 → 垂直でないとバランスが保てない など
|
|
まとめる
|
7 本時の学習について振り返る。
・めあてについて、学習してわか
ったことをまとめる。
・適用問題をする。
・次時の学習内容を確かめる。 |
◇直方体の面と面の垂直、平行の関係を理解している。
【数量や図形についての知識・理解】
〔ワークシート〕 |
○グループや全体の話し合いで「なるほど」と感じたことについて書くように促す。
○辺と辺との関係について学習することを伝える。 |