| ア |
結果の概要 |
|---|
| |
|
| |
各学年ごとに教科の正答率について到達基準との比較を示す。
 |
(ア) |
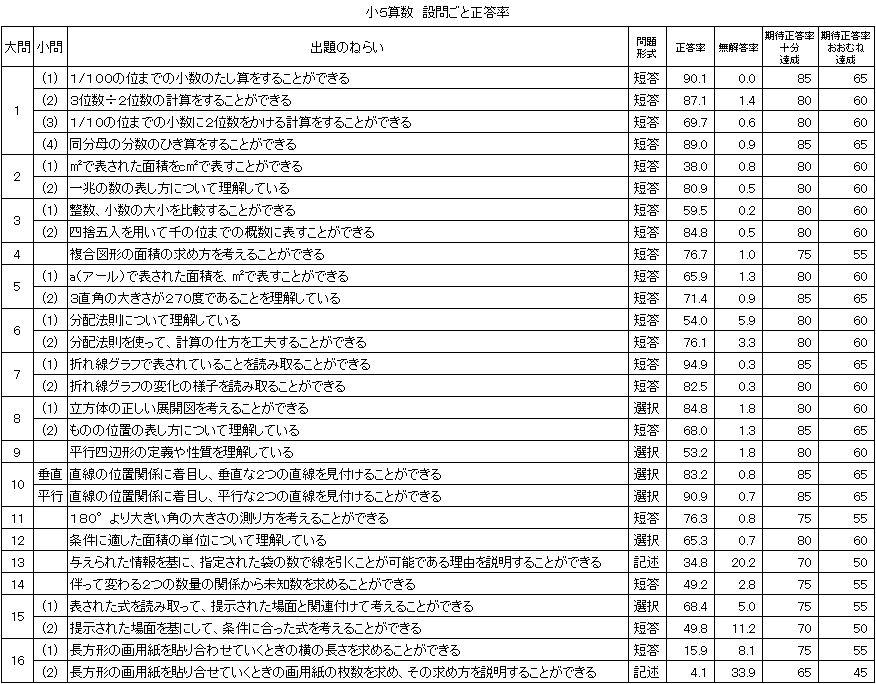
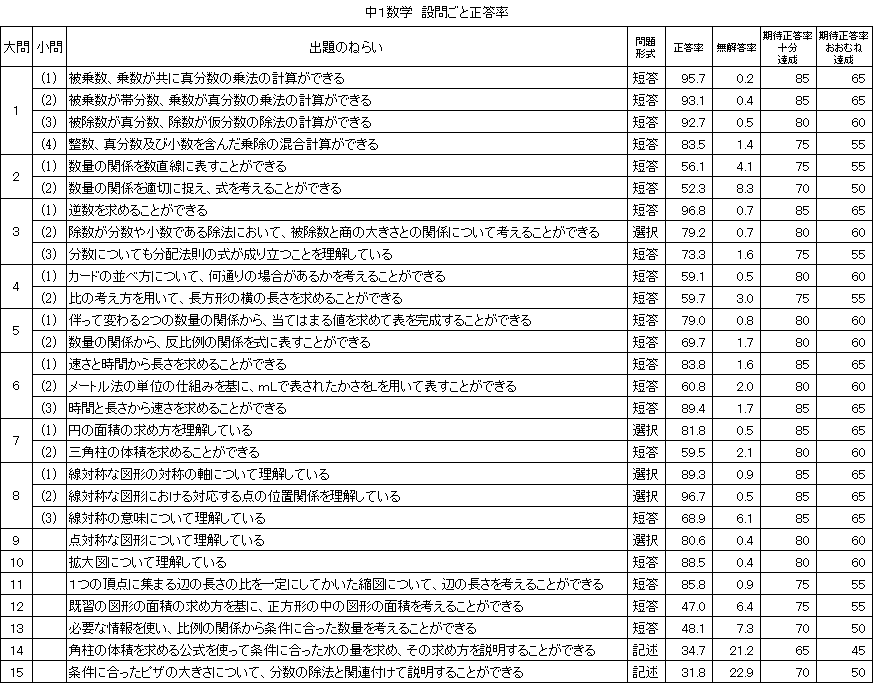
教科及び設問ごと正答率 |
| |
|
| |
|
| |
|
| |
|
(イ) |
評価の観点別正答率
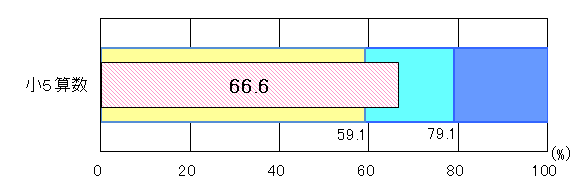
①小学5年生
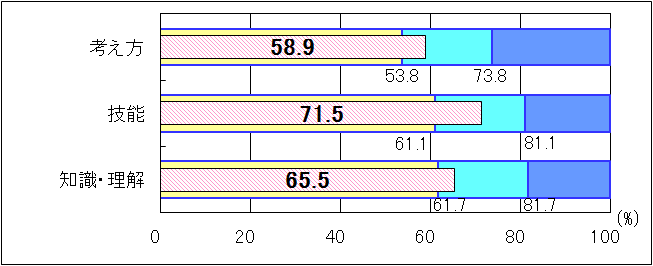 |
図1 H25年度(小学5年生算数)評価の観点別正答率
|
「考え方」「技能」「知識・理解」の全ての観点で「おおむね達成」の基準を上回った。しかし、課題として次の2点が挙げられる。
○「考え方」において、与えられた情報を基に、考えた理由を説明する力。
○「知識・理解」において、平行四辺形の定義や性質の理解。
|
| |
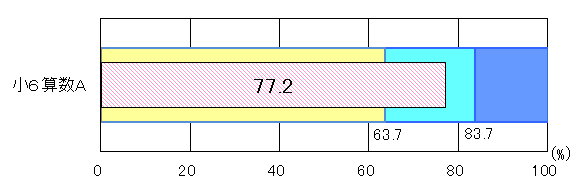
②小学6年生
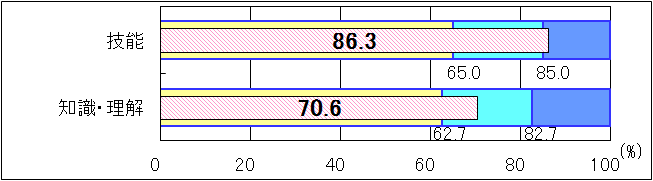 |
図2 H25年度(小学6年生算数A)評価の観点別正答率 |
「技能」は、「十分達成」の到達基準85.0を1.3ポイント上回り、「知識・理解」は、「おおむね達成」の到達基準62.7を7.9ポイント上回った。「技能」においては、四則演算を行う設問の中に、その正答率が90.0を越えている設問もあった。しかし、「知識・理解」における課題として、次の2点が挙げられる。
○単位量当たりの大きさを求める除法の式の意味の理解。
○1a(1アール)の面積と等しい正方形の一辺の長さの理解。
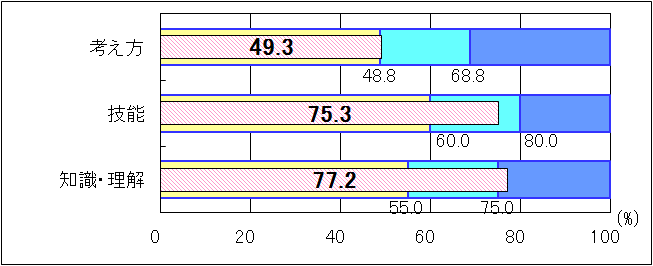 |
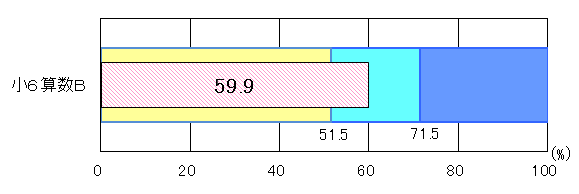
図3 H25年度(小学6年生算数B)評価の観点別正答率
|
「考え方」「技能」では、「おおむね達成」の基準を上回り、「知識・理解」では、「十分達成」の到達基準75.0を2.2ポイント上回った。しかし、「考え方」における課題として、次の2点が挙げられる。
○単位量当たりの大きさなどに着目して、2つの数量の関係の求め方を説明する力。
○表から数値を適切に取り出して、2つの数量の関係が比例の関係ではないことを説明する力。
課題として、次の2点が挙げられる。
○既習の図形の求め方を基に、正方形の中の図形の面積を考える力。
○条件に合ったピザの大きさについて、式と図を関連付けて説明する力。
|
| |
| ③中学1年生 |
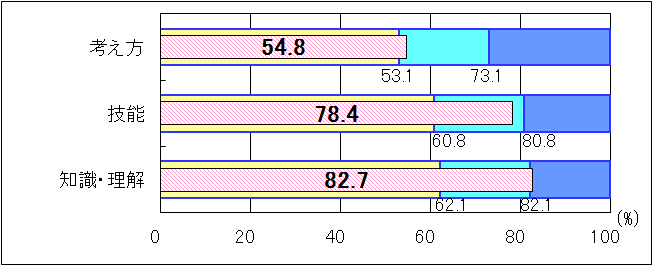 |
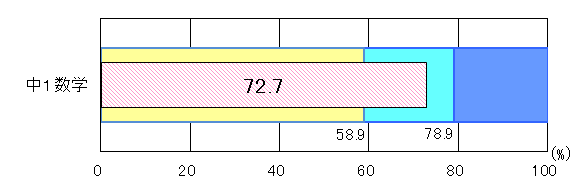
図4 H25年度(中学1年生数学)評価の観点別正答率 |
「考え方」「技能」では、「おおむね達成」の基準を上回り、「知識・理解」では、「十分達成」の到達基準82.1を0.6ポイント上回った。「考え方」における
|
(ウ) |
内容・領域別正答率
内容・領域別正答率においては、「量と測定」「図形」では全ての学年において「おおむね達成」の基準を上回る結果であった。小学6年生算数Bと中学1年生数学における「図形」では、「十分達成」の基準を上回る結果となった。一方、「数と計算」においては、小学6年生算数Bにおいて「おおむね達成」の到達基準50.0を0.5ポイント下回り、「数量関係」では、小学5年生において「おおむね達成」の到達基準56.1を1.1ポイント下回った。
①小学5年生
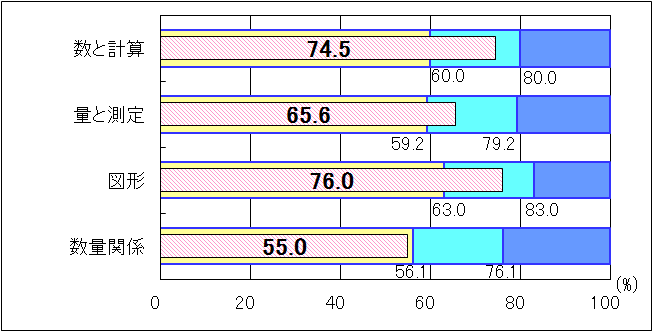 |
図5 H25年度(小学5年生算数)内容・領域別正答率
|
「数と計算」「量と測定」「図形」では、「おおむね達成」の基準を上回る結果であったが、「数量関係」においては、「おおむね達成」の到達基準56.1を1.1ポイント下回った。「考え方」における課題として、次のことが挙げられる。
○長方形の画用紙を貼り合わせていくときの画用紙の枚数を求め、その求め方を説明する力。
|
| |
②小学6年生
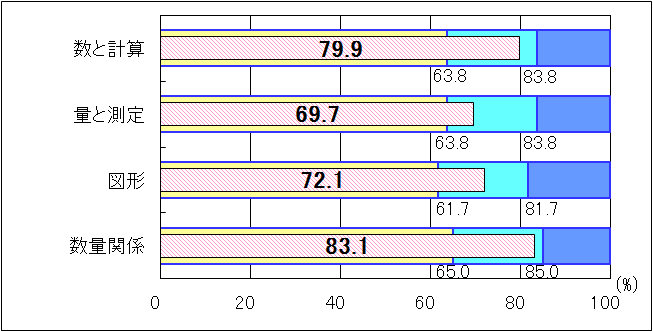 |
図6 H25年度(小学6年生算数A)内容・領域別正答率
|
全ての領域で、「おおむね達成」の基準を上回る結果であった。「数量関係」においては、( )を使って整数の計算をする設問は、「十分達成」の期待正答率85.0を9.6ポイント上回る結果であった。「量と測定」における課題として、次のことが挙げられる。
○単位量当たりの大きさを求める式についての理解。 |
| |
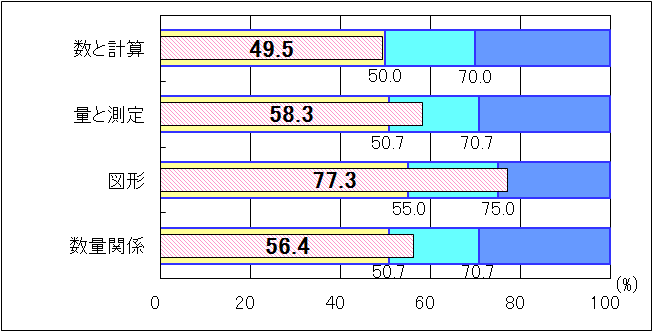 |
図7 H25年度(小学6年生算数B)内容・領域別正答率
|
「量と測定」「数量関係」においては、「おおむね達成」の基準を上回り、「図形」では、「十分達成」の到達基準75.0を2.3ポイント上回る結果であった。しかし、「数と計算」においては、「おおむね達成」の到達基準50.0を0.5ポイント下回る結果となった。「数と計算」における課題として、次のことが挙げられる。
○3つの買い方の中から最も安くなる買い方を選択し、その選択が正しい理由を説明する力。
|
| |
③中学1年生
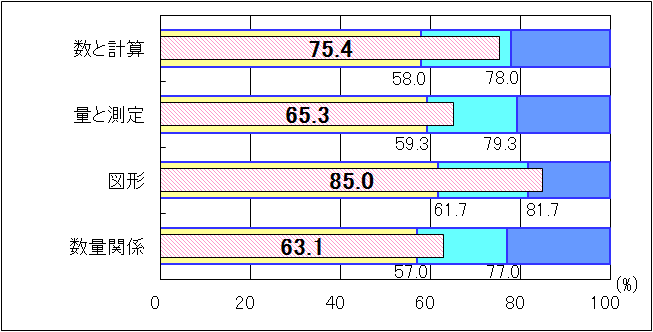 |
図8 H25年度(中学1年生数学)内容・領域別正答率
|
全ての領域で、「おおむね達成」の基準を上回り、「図形」においては、「十分達成」の到達基準81.7を3.3ポイント上回る結果であった。「量と測定」における課題として、次のことが挙げられる。
○角柱の体積を求める公式を使って、条件に合った水の量を求め、その求め方を説明する力。
|
| |
|
| イ |
|
|---|
| |
|
| |

|
| |
知識・技能の定着の状況を把握するために「基礎的・基本的問題」における正答率を比較し、考察する。また、筋道を立てて考え、表現する力の定着の状況を把握するために、平成24年度に課題として挙げられていた「活用」における問題の正答率を比較し、考察する。小学6年生については、「基礎的・基本的問題」における正答率は算数Aで比較し、「活用」における問題の正答率は算数Bで比較する。 |
| (ア) |
「基礎的・基本的問題」の経年比較
①小学5年生
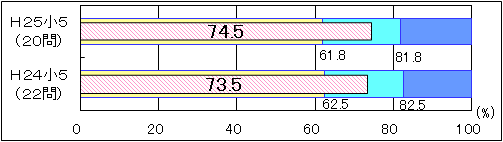 |
図9 H24・H25年度(小学5年生算数)「基礎的・基本的問題」の
正答率の経年比較 |
「基礎的・基本的問題」の正答率については、平成24年度の正答率は73.5で、「おおむね達成」の到達基準62.5を11.0ポイント上回っていた。平成25年度の正答率は74.5で、「おおむね達成」の到達基準61.8を12.7ポイント上回った。内容・領域別に見てみると、平成25年度は「数と計算」の1/100の位までの小数のたし算をする設問において、「十分達成」の期待正答率を上回った。しかし、「量と測定」の㎡で表された面積をc㎡で表す設問において、「おおむね達成」の期待正答率を下回った。 |
| |
|
| |
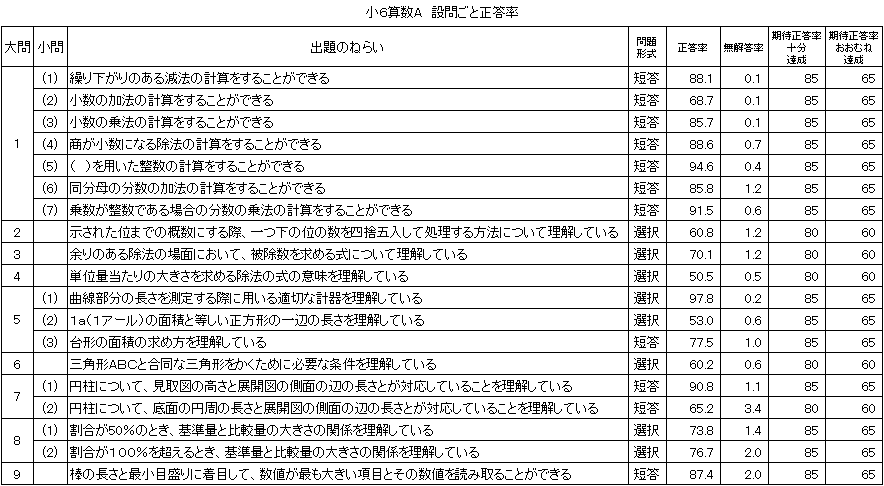
②小学6年生算数A
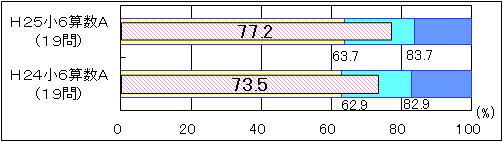 |
図10 H24・H25年度(小学6年生算数A)「基礎的・基本的問題」の
正答率の経年比較 |
「基礎的・基本的問題」の正答率については、平成24年度の正答率は73.5で、「おおむね達成」の到達基準62.9を10.6ポイント上回っていた。平成25年度の正答率は77.2で、「おおむね達成」の到達基準63.7を13.5ポイント上回った。内容・領域別に見てみると、平成25年度は「数量関係」の( )を用いた整数の計算をする設問において、「十分達成」の期待正答率を上回った。しかし、「量と測定」の1a(1アール)と等しい面積になる正方形の一辺の長さを求める設問において、「おおむね達成」の期待正答率を下回った。 |
| |
|
|
③中学1年生
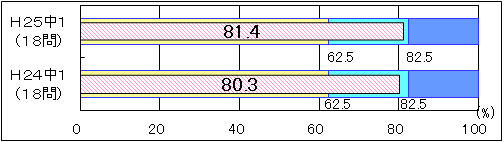 |
図11 H24・H25年度(中学1年生数学)「基礎的・基本的問題」の
正答率の経年比較
|
「基礎的・基本的問題」の正答率については、平成24年度の正答率は80.3で、「おおむね達成」の到達基準62.5を17.8ポイント上回っていた。平成25年度の正答率は81.4で、「おおむね達成」の到達基準62.5を18.9ポイント上回った。平成24年度と比較すると正答率は1.1ポイント上回っている。内容・領域別に見てみると、平成25年度は、「図形」において線対称な図形における対応する点の位置関係の理解を問う設問と「数と計算」の逆数を求める設問において、「十分達成」の期待正答率を上回った。しかし、「量と測定」の三角柱の体積を求める設問において、「おおむね達成」の期待正答率を下回った。 |
| |
|
| (イ) |
「活用」に関する問題の経年比較
①小学5年生
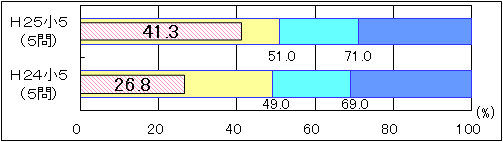 |
図12 H24・H25年度(小学5年生算数)「活用」に関する問題の
正答率の経年比較 |
「活用」に関する問題の正答率については、平成24年度の正答率は26.8で、「おおむね達成」の到達基準49.0を22.8ポイント下回っていた。また、平成25年度の正答率は41.3で、「おおむね達成」の到達基準51.0を9.7ポイント下回った。平成24年度と同様に、「活用」に関する問題においては課題が見られる。内容・領域別に見てみると、平成25年度は「数と計算」において与えられた情報を基に、指定された袋の数で線を引くことが可能である理由を説明する設問、「数量関係」においては長方形の画用紙を貼り合わせていくときの横の長さを求める設問において、「おおむね達成」の期待正答率を下回った。 |
| |
|
| |
②小学6年生算数B
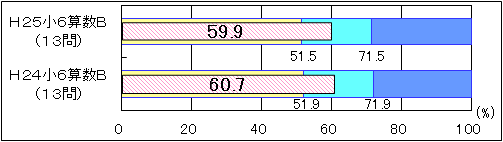 |
図13 H24・H25年度(小学6年生算数B)「活用」に関する問題の
正答率の経年比較 |
「活用」に関する問題の正答率については、平成24年度の正答率は60.7で、「おおむね達成」の到達基準51.9を8.8ポイント上回っていた。また、平成25年度の正答率は59.9で、「おおむね達成」の到達基準51.5を8.4ポイント上回った。内容・領域別に見てみると、平成25年度は「数と計算」と「量と測定」において単位量当たりの大きさなどに着目して、2つの数量の関係の求め方を記述する設問、「数量関係」において示された式に数値を当てはめて計算し、計算の結果の大小を基に判断する設問において、「おおむね達成」の期待正答率を下回った。 |
| |
|
|
③中学1年生
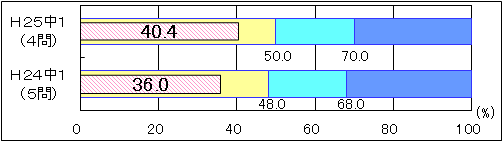 |
図14 H24・H25年度(中学1年生数学)「活用」に関する問題の
正答率の経年比較
|
「活用」に関する問題の正答率については、平成24年度の正答率は36.0で、「おおむね達成」の到達基準48.0を12.0ポイント下回っていた。また、平成25年度の正答率は40.4で、「おおむね達成」の到達基準50.0を9.6ポイント下回った。平成24年度と同様に、「活用」に関する問題においては課題が見られる。内容・領域別に見てみると、平成25年度は「数と計算」においては条件に合ったピザの大きさについて、式と図を関連付けて説明する設問、「量と測定」においては角柱の体積を求める公式を使って条件に合った水の量を求め、その求め方を説明する設問、「数量関係」においては必要な情報を使い、比例の関係から条件に合った数量を考える設問において「おおむね達成」の期待正答率を下回った。 |
| |
|
| |
|
| ウ |
設問ごとに見た傾向と指導改善の手立て |
|---|
| |
|
| |
「基礎的・基本的な知識・技能の定着」と「数学的な思考力・判断力・表現力の育成」の2つの視点から、平成25年度の調査で、正答率が「おおむね達成」の期待正答率を下回った主な設問について考察する。 |
| |
|
傾向1 |
基礎的・基本的問題の中で、「量と測定」の学習内容の定着に課題がある。
[小学5年生 大問2の(1)]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率60.0に対して、正答率は38.0であり、22.0ポイント下回った。1m=100㎝であることや、1㎡は、1辺が1mの正方形の面積であることの理解が図れていないこと、100×100の計算ができなかったことなどが要因であると考えられる。
○ 指導改善の手立て
指導に当たっては、まず、1m=100㎝であることを理解させ、1㎡は、1辺が100cmの正方形の面積であることを確認する。その上で、模造紙を使って面積が1㎡である正方形を作ったり、出来上がったその正方形と面積が1c㎡である正方形を比べたりする活動を通して、面積の量感を育てることが大切である。
[小学6年生算数A 大問4]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率60.0に対して、正答率は50.5であり、9.5ポイント下回った。示された表の中の情報と単位量当たりの大きさを求める式とを適切に対応させることができなかったことが要因であると考えられる。
○ 指導改善の手立て
指導に当たっては、2つの量のどちらを単位量とするかによって、混み具合は数値が大きい方が混んでいる場合と、数値が小さい方が混んでいる場合があるので、数値の意味を理解して判断できるようにさせる。その際、問題場面を図に表させ、単位量当たりの大きさを求める式と図とを対応させて考える活動を積極的に取り入れることが大切である。 |
| |
[中学1年生 大問7の(2)]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率60.0に対して、正答率は59.5であり、0.5ポイント下回った。この設問では、底面となる直角三角形の10cmの斜辺が余計となる。このため縦4cm、横10cmの長方形を底面と考えてしまい、「直角三角形が底面である」と正しく捉えられなかったことが要因であると考えられる。
○ 指導改善の手立て
指導に当たっては、角柱の体積を求める公式の確実な定着を図る必要がある。その際に、直方体や立方体の体積の求め方を基にして角柱の場合の体積の求め方を考えさせることが大切である。具体的には、底面から高さを1cmとり、そこで切った立体の体積を考えさせ、その体積を高さの分だけ倍にする考えを用いて体積を導き出させる。このため、角柱の底面がどこであるのかを把握させる必要がある。そこで、授業では立体模型を使って底面を探し出す活動を取り入れることが大切である。 |
| |
|
傾向2 |
基礎的・基本的な知識・技能を活用することに課題がある。
[小学5年生 大問16の(1)]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率55.0に対して、正答率は15.9であり、39.1ポイント下回った。画用紙を横一列に貼り合わせるときに、のりしろの長さを全体から引いて考えることができなかったことが要因として考えられる。
○ 指導改善の手立て
指導に当たっては、画用紙が1枚の場合、2枚の場合、3枚の場合と、具体物を使って、実際に操作させたり、既に分かっていることを図にかきこませたりする活動を取り入れ、変わり方のきまりを見付けさせていくことが大切である。その上で、このような活動を通して見付けたきまりをノートに書かせたり、友達と説明し合ったりさせることで、見付けたきまりを整理し、明確にさせていくことが大切である。
[小学5年生 大問16の(2)]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率45.0に対して、正答率は4.1であり、40.9ポイント下回った。問題文と示された図から問題場面を把握することや伴って変わる2つの数量の関係を適切に捉えることができなかったことが要因であると考えられる。
○ 指導改善の手立て
指導に当たっては、伴って変わる2つの数量について、操作活動や表に表すなどの活動を通して見付けた変わり方のきまりを活用して、問題解決に取り組ませることが大切である。また、学んだことや見付けたきまりを学習に活用する態度を育成することも大切である。
[小学6年生算数B 大問4の(1)]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率50.0に対して、正答率は40.8であり、9.2ポイント下回った。単位量当たりの大きさの考えに着目して、筋道を立てて考えることができなかったことが要因として考えられる。
○ 指導改善の手立て
指導に当たっては、筋道を立てて考え、表現させるために、式だけで考えを表現させるのではなく、言葉で立式した根拠を書かせることで、何を求めようとしているのかを明確にさせることが大切である。
また、単位量当たりの大きさの学習では、2つの数量のうち、その一方をそろえることによって比べることができることに重点をおいて指導に当たる必要がある。
[中学1年生 大問14]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率45.0に対して、正答率は34.7であり、10.3ポイント下回った。直方体の水そうで、高さが4cm上がることで増える水の体積を求めることができなかったり、増える水の体積が容器の体積の何倍になっているのかということまで考えを進めることができなかったりしたことが要因であると考えられる。
○ 指導改善の手立て
この設問は、既に入っている水の体積は考慮する必要がない設問である。指導に当たっては、既に分かっていることを図にかきこませ、問題解決に向けての方法の見通しをもたせる指導が大切である。具体的には、まず、高さが4cm上がることによって増える水の体積を求めればよいことに気付かせる。次に、それが容器の体積の何倍になっているのかを考えさせる。このように、順序よく考え、見通しをもって問題解決に当たる態度を育成することが大切である。
[中学1年生 大問15]
○ 問題の概要
○ 解答状況
「おおむね達成」の期待正答率50.0に対して、正答率は31.8であり、18.2ポイント下回った。言葉と図を基に、式の意味を読み取ることができなかったことが要因として考えられる。
○ 指導改善の手立て
指導に当たっては、式の意味を読み取らせるために、式と図を関連付けて考える活動を仕組むことが大切である。問題場面を捉えさせる際には、設問の中の情報を基に、自分なりに図に表させることが有効である。そして、その図を基にして、式の意味を説明させることで、筋道を立てて考えたことを表現し、説明する力を育成することが大切である。 |
| |
|
| エ |
これからの指導に向けて |
|---|
| |
|
| |
今回の調査によって、知識・技能の定着と筋道を立てて考え、表現する力に課題があることが分かった。知識・技能の定着を図るためには、授業や家庭学習において、計算練習をさせることはもちろんであるが、算数の用語の意味を理解させ、考えたことを式だけでなく言葉や図や表も使って表現する力の定着も図る必要がある。また、筋道を立てて考え、表現する力の育成においては、特に、式から読み取ったことを言葉や図や表を関連付けて説明する力が十分に育っていないことが課題として考えられる。また、基礎的・基本的な知識・技能を活用する力にも課題が見られた。そこで、これからの指導に向けて、教師意識調査結果を踏まえつつ、次の4点に留意しながら授業に取り組んでいくことが大切であると考える。
(ア) 基礎的・基本的な知識・技能の定着を図る。
基礎的・基本的な知識・技能の定着を図るためには、授業の始めに前時の内容を振り返ったり、家庭学習として学習用プリントを配布したりする際に、児童が正しい計算方法を身に付け、算数の用語を理解できているかを個別に確認しておくことが大切である。誤った計算方法を覚えた児童が、家庭学習で多くの練習問題を解けば、誤った計算方法が定着してしまうことになる。このようなことを防ぐために、授業の終末において、児童に練習問題を解かせる際には、教師がたとえ1問であっても、全児童が正しい計算方法を身に付けているかどうかや算数の用語を理解できているかどうかを確認することが大変重要である。単元によっては、基礎的・基本的な知識・技能の定着を図る学習用プリント(基本問題)が、佐賀県教育センターのWebページからダウンロードできるので、授業や家庭学習で使う学習用プリントとして利用してほしい。
(イ) 考えたことを式だけでなく言葉や図や表も使って表現する活動を取り入れる。
課題解決の過程においては、式だけでなく、言葉や図や表も使って考えを表現させることが大切である。指導に当たっては、既に分かっていることを基に、考えたことを式だけでなく、言葉や図や表も使って表す活動を取り入れる。言葉や図や表を使って考えを表現させる際には、以下のようなことを大切にしたい。
| 言葉 |
言葉を使うよさは、順序立てて考えを表現できることである。また、何を求めようとしているのかを明確にすることができる。式だけでは表現できない立式の根拠や式の意味を表現させていくことが大切である。 |
| 図 |
図を使うよさは、問題場面を把握しやすくすることである。算数で扱う図については、テープ図、線分図、関係図、面積図など多くの種類がある。これらの図は、かき方の指導を行わずしてかけるようになるものではない。発達段階に応じて、それらの図を順序よくかくための適切な指導が必要である。 |
| 表 |
表を使うよさは、複雑な数量の関係を簡潔に表すことができることである。関数の考えを必要とする単元においては、表に表すことで変わり方のきまりを見付けやすくすることができる。表をかかせる際には、伴って変わる2つの数量に着目させることが大切である。 |
以上のことから、式だけでなく、言葉や図や表も使って考えを表現することのよさを実感させるような指導を行うことで、筋道を立てて考えを表現する力の育成が期待できる。
(ウ) 式から読み取ったことを言葉や図や表を関連付けて説明する活動を取り入れる。
児童にとって、立式の根拠や式の意味を読み取ることは、非常に難しいことである。そこで、立式の根拠や式の意味を捉えさせるためには、式と言葉や図や表を関連付けて考えさせることが有効である。指導に当たっては、考え方が複数ある問題において、小集団や学級全体で考えさせる際に、式のみを取り上げてその意味を説明する活動を仕組むことは効果的である。その際、立式の根拠や式の意味について、式と言葉や図や表を関連付けながら説明するよう指導することが大切である。このような活動を通して、立式の根拠や式の意味を筋道を立てて説明する力が育つと考える。
○ 教師意識調査結果から
教師意識調査(28)の「算数で、児童が問題について、目的意識をもって、具体物や言葉、数、式、図、表、グラフなどを用いて考え、自分の考えをもつ活動を取り入れた授業を行っていますか」の質問に対して、「多くの単元で行っている」「半分程度の単元で行っている」と回答した教師の割合は、合わせて86.9%であった。佐賀県内の算数の授業で、約9割の教師が、半分を越える単元において上記の活動を取り入れていることが分かる。この活動においては、上記(イ)、(ウ)の視点をもって指導に当たることが大切である。式と言葉や図や表を使って考えを表現し、それらを関連付けて考えることで根拠を明らかにできるよさを児童に実感させることが、この活動を一層充実したものにすると考える。
(エ) 算数の学習や日常の事象において、基礎的・基本的な知識・技能を活用する課題の設定をする。
児童が、算数の授業で身に付けた基礎的・基本的な知識・技能を活用して、算数の学習や日常の事象における課題を解決することは、算数を学ぶよさを実感することへとつながる。そこで、算数の学習においては、本時の学習がどのような既習事項と関連しているかを児童に捉えさせることが大切である。そのためには、これまでに児童は何を学び、何を学んでいないのかを明らかにし、系統性を踏まえて指導していく必要がある。また、児童が学んだことを振り返りやすいように掲示物の工夫をしたり、見やすく整理されたノートをモデルとして示したりすることも有効である。単元末や学期末では、学んだことが身の回りの生活場面においてどのように使われているかを探る活動を取り入れ、算数の学習内容と日常の事象を関連させることが大切である。算数の学習内容と日常の事象を関連付けた発展的な問題を積極的に取り入れることは、基礎的・基本的な知識・技能を活用する力の育成に効果的だと考える。その際、単元によっては、数学的な思考力・判断力・表現力を育む学習用プリント(数学的な思考力・判断力・表現力を育む問題)が、佐賀県教育センターのWebページからダウンロードできるので、指導のポイントを参考にして、活用してほしい。 |
| |
|
| オ |
授業実践に参考となるリンク |
|---|
| |
|
| |
 |
| |
|
| |
 |