| ア |
結果の概要 |
| |
各学年ごとに教科全体の正答率について到達基準との比較を示す。
 |
(ア) |
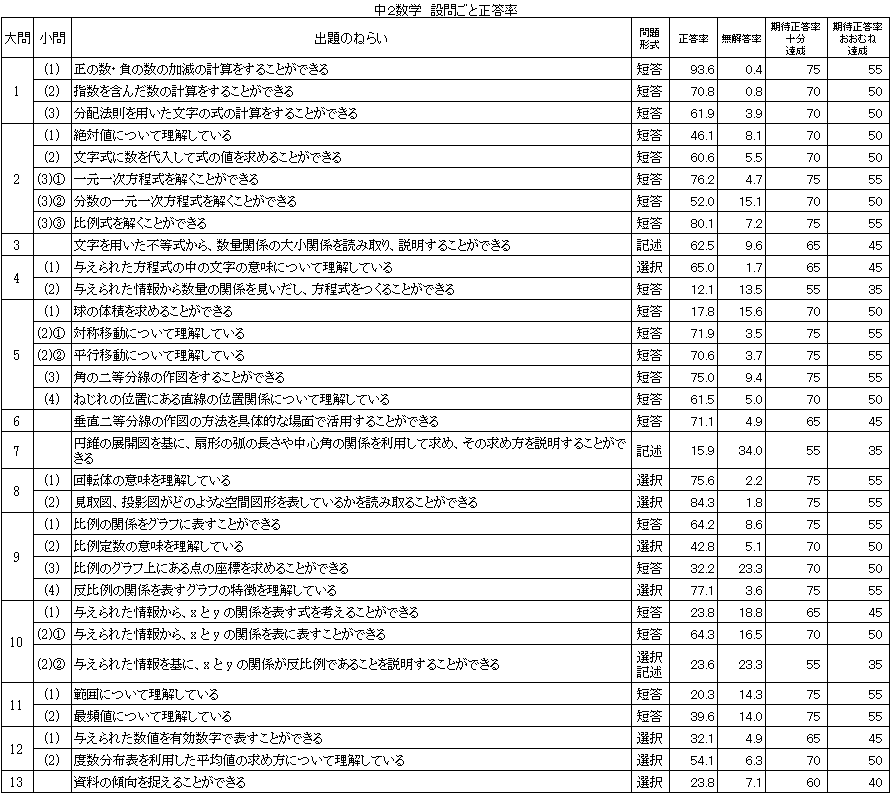
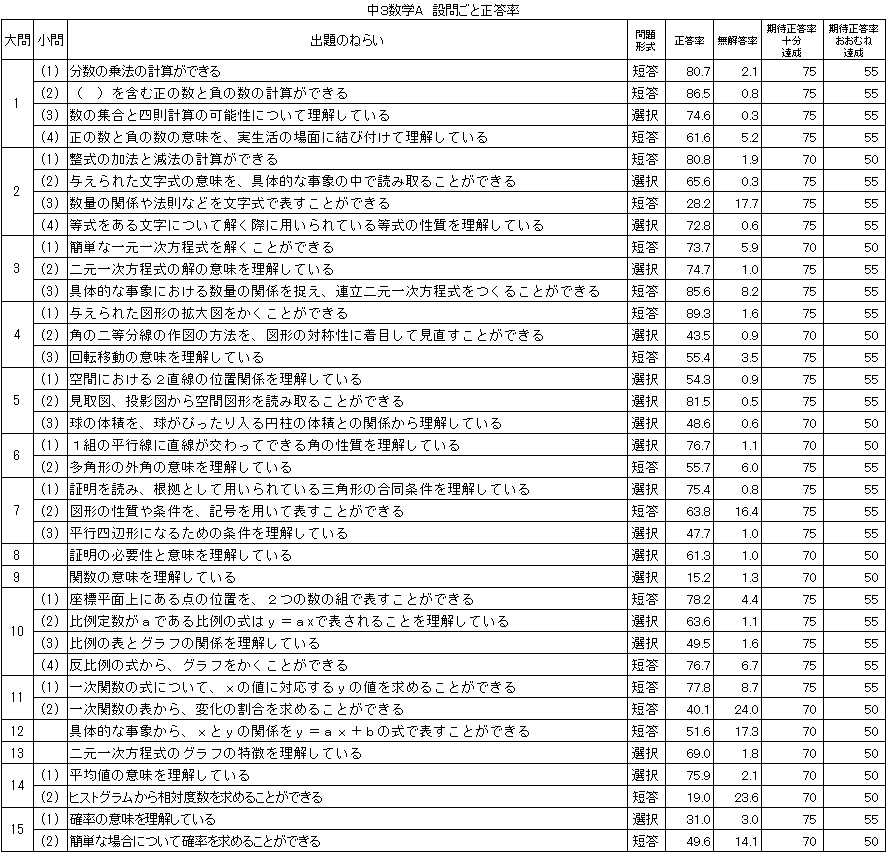
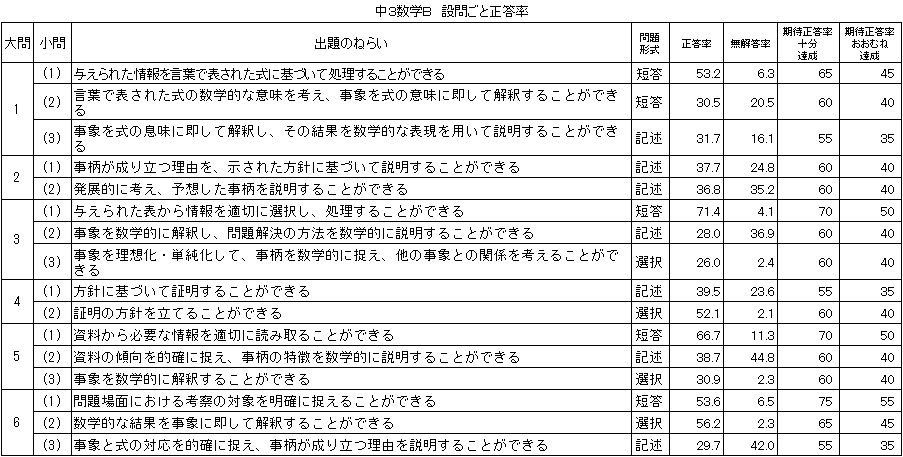
教科及び設問ごと正答率 |
| |
|
| |
|
(イ) |
評価の観点別正答率
中学2年生
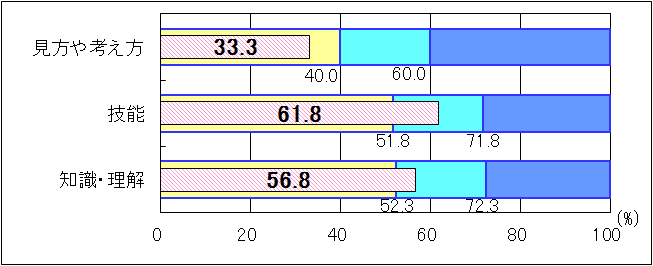 |
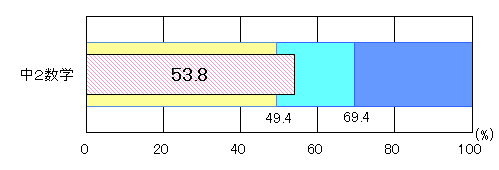
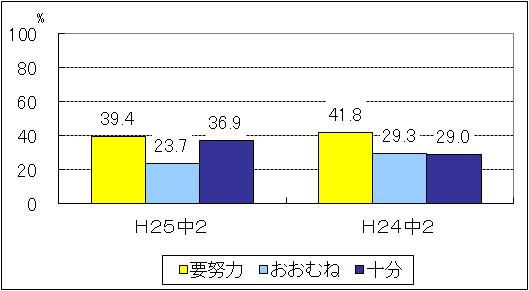
| 図1 H25年度(中学2年生数学)評価の観点別正答率 |
「技能」については、「おおむね達成」の基準を10.0ポイント上回ったが、「球の体積を求めること」や「比例のグラフ上の点の座標を求めること」には課題が見られた。「知識・理解」についても、「おおむね達成」の基準を4.5ポイント上回ったが、「絶対値や範囲、最頻値などの用語に関すること」や「比例定数の意味に関すること」には課題が見られた。「見方や考え方」については、「おおむね達成」の基準を6.7ポイント下回り、特に「与えられた情報から数量の関係を見いだし、方程式をつくること」「円錐の展開図を基に、扇形の弧の長さや中心角の求め方を説明すること」「与えられた情報を基に、xとyの関係が反比例であることを説明すること」などの設問の正答率で「おおむね達成」の基準を10.0ポイント以上下回っていた。
|
| |
中学3年生
①A問題
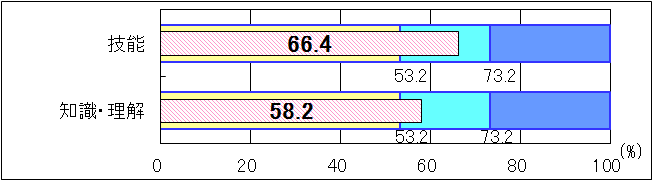 |
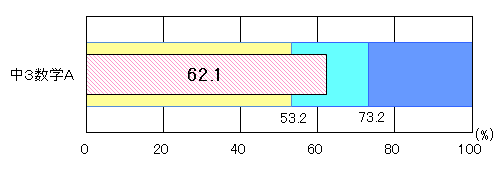
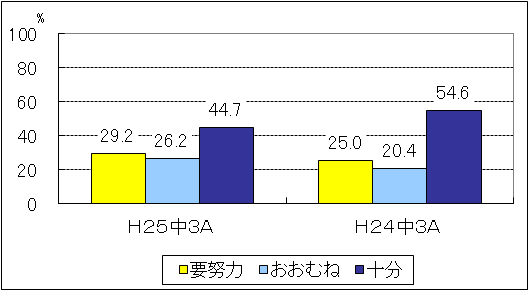
| 図2 H25年度(中学3年生数学A)評価の観点別正答率 |
中学2年生と同様に、「技能」と「知識・理解」は共に「おおむね達成」の基準を上回った。しかしながら、「技能」については、「数量の関係や法則を文字式で表すこと」や「変化の割合、相対度数、確率を求めること」に課題が見られた。「知識・理解」については、「角の二等分線の作図の方法を、図形の対称性に着目して見直すこと」や「関数や確率の意味に関すること」に課題が見られた。
|
| |
②B問題
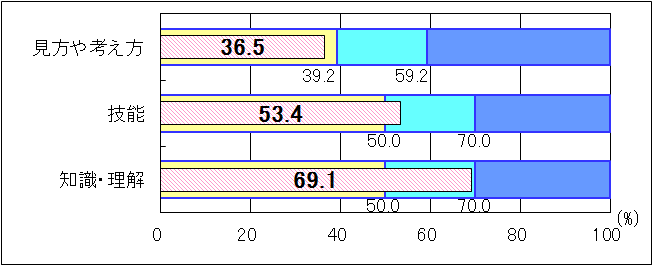 |
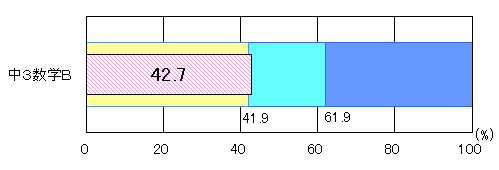
| 図3 H25年度(中学3年生数学B)評価の観点別正答率 |
中学2年生と同様に、「技能」と「知識・理解」は共に「おおむね達成」の基準を上回ったが、「見方や考え方」は「おおむね達成」の基準を2.7ポイント下回った。「見方や考え方」については、「結果を数学的な表現を用いて説明すること」「事柄が成り立つ理由を説明すること」「問題解決の方法を説明すること」などの数学的な表現を用いて説明することに課題が見られた。「技能」については、「問題場面における考察の対象を明確に捉えること」に課題が見られた。
|
| |
|
(ウ) |
内容・領域別正答率
中学2年生
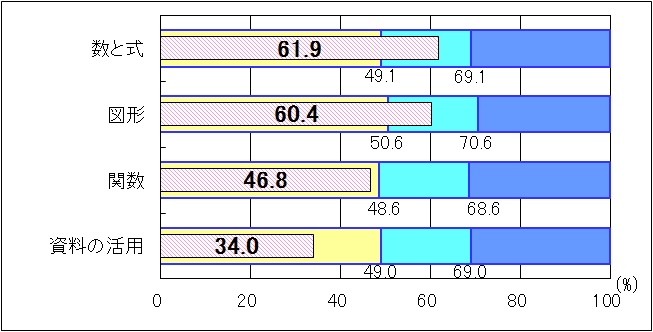 |
| 図4 H25年度(中学2年生数学)内容・領域別正答率 |
「数と式」については、「おおむね達成」の基準を12.8ポイント上回ったが、「絶対値に関すること」や「与えられた情報から数量の関係を見いだし、方程式をつくること」に課題が見られた。「図形」については、「おおむね達成」の基準を9.8ポイント上回ったが、「球の体積を求めること」や「円錐の展開図を基に、扇形の弧の長さや中心角の求め方を説明すること」に課題が見られた。「関数」については、「比例のグラフ上にある点の座標を求めること」や「反比例であることを説明すること」などの設問で正答率が「おおむね達成」の基準を10.0ポイント以上下回った。また、「資料の活用」については、「資料の傾向を捉えること」や「範囲や最頻値の用語に関すること」などの設問でも正答率が「おおむね達成」の基準を10.0ポイント以上下回っていた。 |
|
中学3年生
①数学A
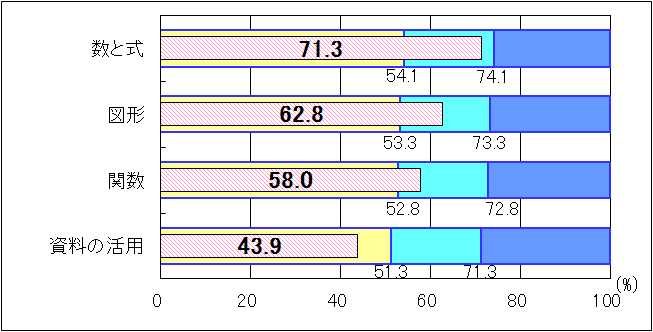 |
| 図5 H25年度(中学3年生数学A)内容・領域別正答率 |
「数と式」については、「おおむね達成」の基準を17.2ポイント上回ったが、「数量の関係や法則などを文字式で表すこと」に課題が見られた。「図形」についても、「おおむね達成」の基準を9.5ポイント上回ったが、「角の二等分線の作図の方法を、図形の対称性に着目して見直すこと」や「球と円柱の体積の比較に関すること」に課題が見られた。「関数」についても、「おおむね達成」の基準を5.2ポイント上回ったが、「関数の意味に関すること」や「一次関数の表から、変化の割合を求めること」に課題が見られた。「資料の活用」については、「おおむね達成」の基準を7.4ポイント下回り、「相対度数や確率を求めること」や「確率の意味に関すること」に課題が見られた。
|
|
②数学B
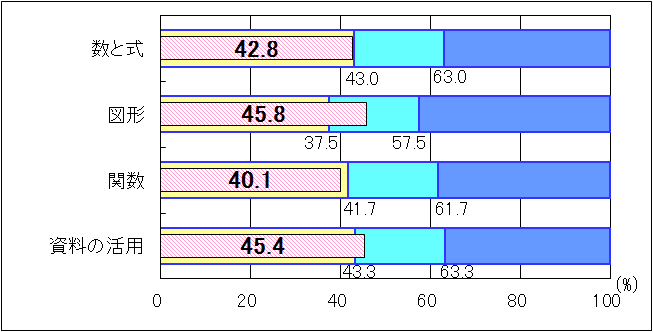 |
| 図6 H25年度(中学3年生数学B)内容・領域別正答率 |
「図形」については、「おおむね達成」の基準を8.3ポイント、「資料の活用」については2.1ポイント上回った。「資料の活用」については、「資料の傾向を的確に捉え、事柄の特徴を数学的に説明すること」に課題が見られた。「数と式」「関数」については、共に「おおむね達成」の基準を下回った。「数と式」では、「事柄が成り立つ理由を説明すること」の2つの設問の無解答率が24.8と42.0で、「予想した事柄を説明すること」の設問の無解答率は35.2であった。「関数」では、「問題解決の方法を説明すること」の設問の無解答率は36.9であった。
|
| |
|
| |
|
| イ |
|
| |
|
| |

中学2年生では、平成24年度の課題であった「基礎的・基本的な問題」と「活用」に関する問題についての変容を考察するために、同一学年の経年比較を行った。中学3年生では、数学Aについては「基礎的・基本的な問題」、数学Bについては記述式の設問を中心に変容を考察するために、同一学年の経年比較を行った。
|
| |
|
(ア) |
「基礎的・基本的問題」の経年比較(同一学年)
中学2年生
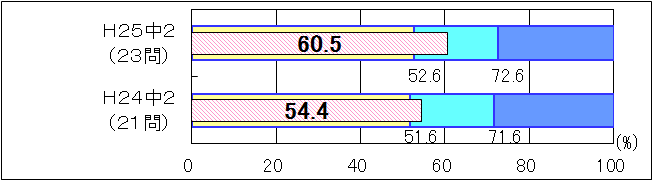 |
図7 H24・H25年度(中学2年生数学)「基礎的・基本的な問題」の正答率の経年比較 |
|
| 図8 H24・H25年度(中学2年生数学)「知識・理解」の到達度分布の経年比較 |
「基礎的・基本的な問題」については、「おおむね達成」の基準を1として、正答率を算出した値で比較すると、平成25年度は平成24年度よりも上回る結果となった(図7)。「知識・理解」について、平成25年度と平成24年度を到達度分布で比較すると、「十分達成」の基準を上回っている生徒の割合は7.9ポイント増加し、「要努力」の生徒の割合は2.4ポイント減少した(図8)。しかしながら、「グラフ上の点の座標に関すること」や「絶対値や最頻値などの用語に関すること」などの知識の定着に平成24年度同様課題が見られる結果となった。 |
中学3年生数学A問題
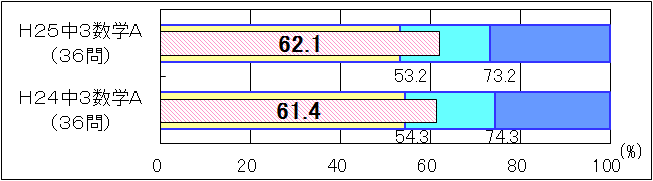 |
図9 H24・H25年度(中学3年生数学A)の正答率の経年比較 |
|
図10 H24年度「数学的な表現・処理」とH25年度「技能」の到達度分布の経年比較
(中学3年生数学A) |
「基礎的・基本的な問題」については、「おおむね達成」の基準や「十分達成」の基準が異なるために、単純に比較することはできないが、正答率で上回る結果となった(図9)。「技能」について、平成25年度と平成24年度の到達度分布で比較すると、「十分達成」の基準を上回っている生徒の割合は9.9ポイント減少し、「要努力」の生徒の割合も4.2ポイント増加している。「数量の関係や法則などを文字式で表すこと」「変化の割合を求めること」「確率を求めること」などの技能を身に付けることに課題が見られた。 |
| |
|
(イ)
|
「活用」に関する問題の経年比較(同一学年)
中学2年生
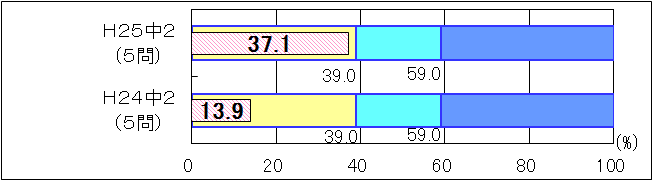 |
図11 H24・H25年度(中学校数学)「活用」に関する問題の正答率の経年比較 |
「活用」に関する問題については、「おおむね達成」の基準及び「十分達成」の基準も等しかったため、比較を行った。平成24年度と比べると、正答率が23.2ポイント上回っている。表1は与えられた情報を基に、数学的な表現を用いて説明するなどの言葉や数を使って説明する設問について比較したものである。また、表2は、数量の関係を見いだし、一元一次方程式をつくる設問について比較したものである。
表1 H24・H25年度(中学2年生数学)記述式の設問の正答率・無解答率の経年比較
|
 |
 |
.
表2 H23・H24・H25年度(中学2年生数学)数量の関係を見いだし、一元一次方程式をつくる設問の正答率・無解答 率の経年比較 |
|
表1、表2より、与えられた情報を基に、数学的な表現を用いて説明するなどの記述式の設問や数量の関係を見いだし、一元一次方程式をつくる設問などの正答率は平成24年度より上回っているが、これまで同様に課題が残る結果となった。 |
|
「活用」に関する問題の経年比較(同一学年)
中学3年生
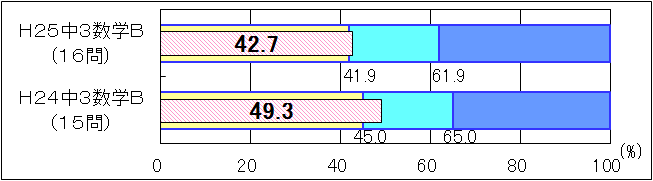 |
図12 H24・H25年度(中学3年生数学「B問題」)の正答率の経年比較 |
数学Bについては、「おおむね達成」の基準及び「十分達成」の基準が異なるために、単純に比較することはできないが、平成25年度も平成24年度も「おおむね達成」の基準を上回っているが、「おおむね達成」の基準を1として正答率を算出して比較すると、平成25年度は平成24年度を下回る結果となった。
表3については、判断した根拠や事柄が成り立つ理由を数学的な表現を用いて説明するなどの記述式の設問について比較したものである。
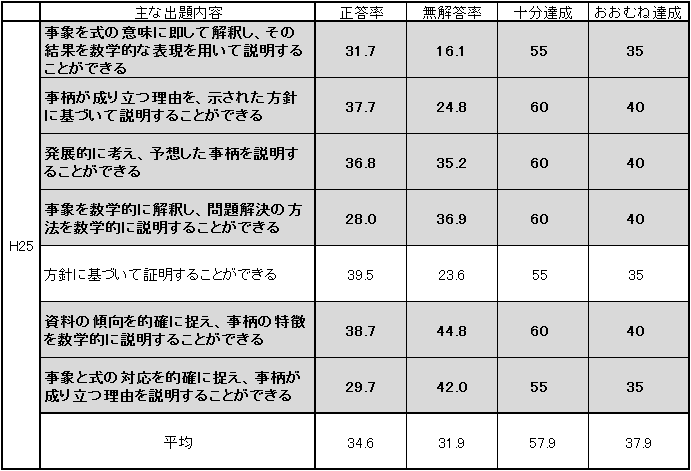
表3 H24・H25年度(中学3年生数学B)記述式の設問の正答率・無解答率の経年比較
|
 |
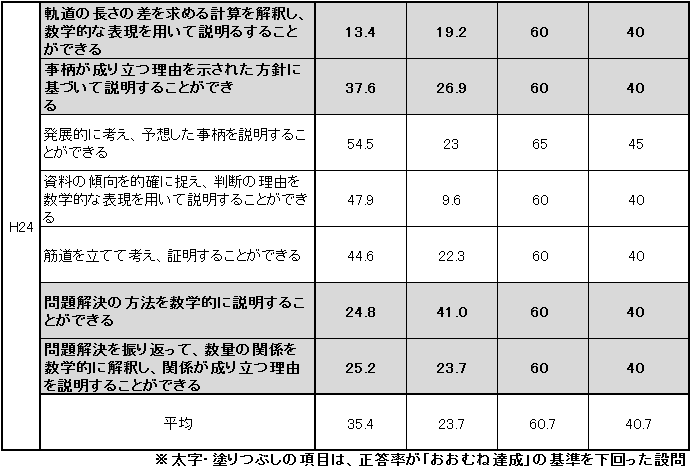 |
「おおむね達成」の基準と「十分達成」の基準が異なるために、単純に比較することはできないが、記述式の平均正答率は平成24年度と比較すると、0.8ポイント下がり、無解答率は8.2ポイント上がる結果となった。また、「おおむね達成」の基準を下回る設問の数も平成24年度より増える結果となった。中学2年生同様に「事柄が成り立つ理由を説明すること」や「問題解決の方法を数学的な表現を用いて説明すること」などの記述式の設問については、平成24年度に引き続き課題を残す結果となった。 |
| ウ |
設問ごとに見た傾向と指導改善の手立て |
| |
|
|
上記の「ア結果の概要」と「イ経年比較」から、特定の基礎的・基本的な知識・技能に関する学習内容、数学的な表現を用いて説明するなどの記述式の学習内容に課題が見られた。これらのことを踏まえて、設問ごとに分析を行うことで、課題をより詳細に把握し、具体的な改善策や方策を提示した。 |
| |
|
傾向1
|
特定の基礎的・基本的な知識・技能に関する学習内容に課題がある。
[中学2年生 大問4]
○ 問題の概要
○ 解答状況
問4(2)は「おおむね達成」の期待正答率35.0に対して、正答率が12.1で、22.9ポイント下回った。線分図を基に、数量の関係を見いだし、一元一次方程式をつくることに課題があると考えられる。
○ 指導改善の手立て
問題の中の数量やその関係から2通りに表される数量を見いだし、文字を用いた式で表すことができるようにすることが大切である。そのために、言葉の式や線分図等を利用して数量の関係を把握したり、式を基にして数量の関係を読み取ったりする活動を設定することが必要であると考える。これらの活動を通して、数量の関係を把握し、文字を用いた式を等号で結ぶことで一元一次方程式をつくることができるようにしたいと考える。この大問では、一元一次方程式をつくる際に、合計の距離について着目する場合と走る合計の人数に着目する場合が考えられる。このように、2つの考え方で一元一次方程式をつくらせるような学習活動を取り入れることが大切であると考える。
[中学2年生 大問9、大問10〕
○ 問題の概要
○ 解答状況
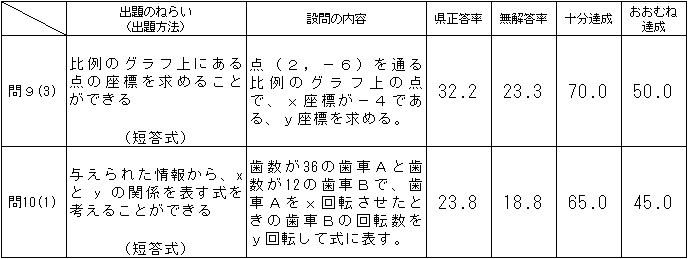
問9(3)は「おおむね達成」の期待正答率50.0に対して、正答率が32.2で、17.8ポイント下回り、問10(1)は「おおむね達成」の期待正答率45.0に対して、正答率が23.8で、21.2ポイント下回った。比例のグラフ上のx座標とy座標の値の組を求めることや身近な事象を数学的に捉え、比例の式に表すことに課題があると考えられる。
○ 指導改善の手立て
比例の式から、グラフをかいた後に、グラフ上にある点のx座標とy座標の値の組がその比例の式を満たすことを、具体的な数値を用いて確認するような学習活動を取り入れる必要があると考える。また、グラフ上にない点について、x座標やy座標の値の組がその比例の式を満たさないことも確認できるようにすることも必要であると考える。日常生活における事象を数理的に考察するために、具体的な数値を用いて、2つの数量の関係について変化や対応の様子を表に表したり、式に表したりする活動が大切である。さらに、観察、操作や実験などの活動に基づいて、2つの数量の関係の変化や対応の様子について表、式、グラフを相互に関連付けて考察する活動を取り入れる必要があると考える。
|
| |
[中学2年生 大問11、大問12、大問13〕
○ 問題の概要
○ 解答状況
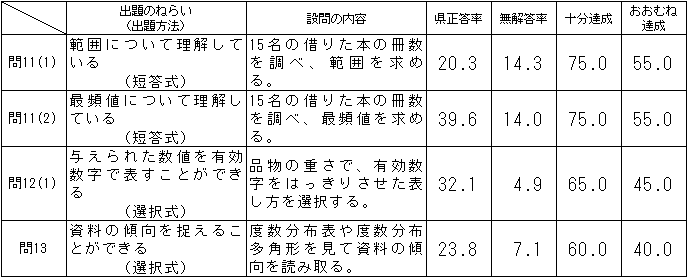
「おおむね達成」の期待正答率は、問11(1)(2)は50.0、問12(1)は45.0、問13は40.0であったが、正答率は、問11(1)は20.3、問11(2)は39.6、問12(1)は32.1、問13は23.8と全て下回った。範囲、最頻値や有効数字などの用語に関することと度数分布表や度数分布多角形の見方などの知識の確実な習得に課題があると考えられる。
○ 指導改善の手立て
日常生活を題材とした問題などを取り上げ、それを解決するために必要な資料を収集し、ヒストグラムや度数分布多角形を作成したり代表値を求めたりして資料の傾向を捉え、その結果を基に説明するという一連の活動を取り入れることが大切である。ヒストグラムや度数分布多角形を作成する際に、インターネットなどを利用して資料を収集することも効果的であると考える。資料の傾向を読み取らせるためには、目的に応じて資料を収集して整理し、中央値、平均値や最頻値などの代表値の必要性と意味を理解したり、資料から代表値を求めたりする学習活動を取り入れる必要があると考える。その際、ヒストグラムの分布が非対称であったり、大きくかけ離れた値があったりすると、平均値は大きく影響を受けるが、中央値や最頻値には影響が出にくいことを確認したり、資料をヒストグラムや度数分布表に整理して代表値を求めたりする学習活動を取り入れることが必要であると考える。数学の用語などの知識については、他者のヒストグラムの特徴についての説明を聞きながら、範囲、最頻値、中央値、平均値などのうち、どの用語の意味を用いたほうがより分かりやすいかを考えることでより理解を深めることもできると考える。 |
| |
[中学3年生数学A 大問2〕
○ 問題の概要
○ 解答状況
問2(3)は「おおむね達成」の期待正答率55.0に対して、正答率は28.2で、26.8ポイント下回った。針金の重さが長さに比例する関係を捉えることに課題があると考える。
○ 指導改善の手立て
数量の関係や法則などを文字を用いた式で表すことは、事象における数量やその関係を一般的に把握したり、形式的に処理を行ったりする際に重要であると考える。そのため、この設問においては、針金の重さが長さに比例する関係であることを捉えさせ、比例式で解決させるようにする必要があると考える。また、文字を具体的な数値に置き換えて考えることができるようにすることも必要であると考える。
[中学3年生数学A 大問11〕
○ 問題の概要
○ 解答状況
問11(2)は「おおむね達成」の期待正答率50.0に対して、正答率は40.1で、9.9ポイント下回った。一次関数の表から、対応する値を選択し、変化の割合を求めることについての知識・技能の習得に課題があると考えられる。
○ 指導改善の手立て
関数の変化の割合はxの増加量に対するyの増加量の割合であり、一次関数においてはその値が常に一定であることを理解させることが大切である。一次関数の変化の割合を求めることができるようにするためには、表でx、yの変化の様子を調べ、変化の割合について理解を深めるようにする必要がある。その際具体的な数値を挙げて、xの増加量やyの増加量を調べ、どの場合でも変化の割合は一定であることを確認したり、一次関数の式で、xの係数と一致していることを確認したりする活動が重要であると考える。また、一次関数の表から変化の割合を求めたり、変化の割合を基にして表に表されていない値を求めたりするなどの学習活動が重要であると考える。
|
| |
[中学3年生数学A 大問15〕
○ 問題の概要
○ 解答状況
問題15(1)は「おおむね達成」の期待正答率55.0に対して、正答率は31.0で、19.0ポイント下回り、問15(2)は期待正答率50.0に対して、正答率は49.6で、0.4ポイント下回った。ある試行を多数回繰り返したとき、全体の試行回数に対するある事象の起こる回数の割合は、ある一定の値に近付くということを理解できていないと考えられる。また、起こり得る場合を樹形図や二次元の表などを利用して整理し、確率を求めることに課題があると考えられる。
○ 指導改善の手立て
確率の意味については、観察や実験などを通して、ある試行を多数回繰り返したときに、ある事象が起こる回数の全体に対する割合が近づいていく値であることを実感を伴って理解できるようにすることが大切である。観察、操作や実験などの具体的な活動を行う際は、答えや解決方法の見通しについて予想をする活動が重要であると考える。予想したことを確かめたり、見直したりする活動を通して、実感を伴って理解できるようにしたいと考える。場合の数を求めるためには、ある視点を決めて、数え忘れや重なりがないように、起こり得る全ての場合を数えることが大切である。そのため、思い付いたまま起こり得る場合を挙げるのではなく、樹形図や二次元の表を用いて起こり得る全ての場合を順序よく数え上げ、問題の条件を基に整理できるようにすることが大切であると考える。 |
傾向2
|
事柄が成り立つ理由や問題解決の方法を数学的な表現を用いて説明することなどの記述式の学習内容に課題がある。
[中学2年生 大問7]
○ 問題の概要
○ 解答状況
問7は「おおむね達成」の期待正答率35.0に対して、正答率は15.9で、19.1ポイント下回った。円錐の底面の半径とその円錐の展開図の扇形の中心角や半径を関連付けて考えることに課題があると考えられる。
○ 指導改善の手立て
円錐の展開図では、その見取図の側面に当たる部分が扇形であることや、底面の円周と扇形の弧の長さが等しいことなど、見取図と展開図の特徴やそれらの関係について関連付けて理解できるようにすることが大切である。そのため、展開図から円錐を実際に組み立て、底面と側面の対応する部分について考察するなどの場面を設定する必要があると考える。円や扇形の学習においては、扇形を円の一部として捉え、弧の長さや面積がその中心角の大きさに比例することを理解できるようにすることが大切である。その考え方を基にして、比例式や方程式を利用した解法などに取り組むことで、数学的な見方や考え方を育てることができると考える。
[中学2年生 大問10]
○ 問題の概要
○ 解答状況
問10(2)②は「おおむね達成」の期待正答率35.0に対して、正答率は23.6で、11.4ポイント下回った。反比例の変化や対応の特徴について、表から値を読み取り、式に表して事柄が成り立つ理由を説明することに課題があると考える。
○ 指導改善の手立て
反比例では、表、式、グラフを相互に関連付けて、伴って変わる2つの数量の変化や対応を観察し、その特徴を見いだして説明する学習活動を取り入れる必要があると考える。反比例の意味については、対応するxとyの値の積が一定であることや、その値が比例定数と等しくなること、xの値を2倍、3倍、4倍・・・とすると、yの値は1/2倍、1/3倍、1/4倍・・・・となることなどを、表と式を関連付けて説明できるようにすることが大切である。その際、対応するxとyの値を式y=a/xに代入し、比例定数を求め、反比例の式を求めることができるようにすることも大切であると考える。
[中学3年生数学B 大問2]
○ 問題の概要
○ 解答状況
問2(2)は「おおむね達成」の期待正答率40.0に対して、正答率は36.8で、3.2ポイント下回った。2けたの自然数と、その数の十の位の数と一の位の数を入れ替えた数の差が9の倍数になることを基に、2けたの自然数と、その数の十の位の数と一の位の数を入れ替えた数の和のように条件を変えて発展的に考え、予想した事柄を説明することに課題があると考える。
○ 指導改善の手立て
発展的に考え、予想することができるようにするために、問題を解決した後、条件を変える視点などを示し、生徒自らが新たな事柄を見いだすような学習活動を取り入れる必要があると考える。また、見いだした事柄を数学的な表現を用いて説明する活動を取り入れることも大切である。条件を変えて発展的に考えさせる際に、条件を変える前の内容について振り返って考えるような機会を設定し、条件を変える前に振り返って考えることの必要性を実感できるようにすることも重要であると考える。
[中学3年生数学B 大問3]
○ 問題の概要
○ 解答状況
問3(2)は「おおむね達成」の期待正答率40.0に対して、正答率は28.0で、12.0ポイント下回った。事象を数学的に解釈し、表、式、グラフなどを利用して、問題解決の方法を数学的に説明することに課題があると考えられる。
○ 指導改善の手立て
与えられた表やグラフを用いて、データでは与えられていない温度に対応する時間を推測する方法を説明する設問で、事象を数学的に解釈して、問題解決の方法を説明することが求められている。そのため、日常的な事象を形式的に処理して考えることや事象の変化や対応の様子を一次関数とみなして考える学習活動が大切であると考える。変化や対応の様子を捉える際には、これまでに学習した内容を基に、変化の割合が一定であることやグラフ上の点の並びを見て一次関数として考えることに気付くような場面を設定することも大切であると考える。一次関数y=ax+bとして考える際に、xの値とそれに対応するyの値がそれぞれ何を表しているかを把握させ、xの値やyの値を式に代入して対応する値を求めたり、変化の割合を利用して求めたりする際に、どのようして求めるのかという問題解決の方法まで説明する学習活動を取り入れることが重要であると考える。
|
| |
|
| |
|
| エ |
これからの指導に向けて |
| |
|
| |
今回の調査において明らかになったことは、「文字を用いて式に表すこと」「表、式、グラフの関連に関すること」「中央値、最頻値などの代表値、相対度数、確率を求めること」などの基礎的・基本的な知識・技能を身に付けさせることと「事象の中から数量の関係を読み取って、方程式をつくること」「事柄が成り立つ理由を説明すること」「事柄を調べる方法や手順を説明すること」などの数学的な見方や考え方を育てることに課題があることが分かった。そのため、これからの指導に向けて、以下の3点に留意しながら指導改善を図っていく必要があると考える。
(ア)日常生活の事象を数理的に考察する学習活動の充実
日常生活の事象を数理的に考察する力を高める必要がある。そのために、日常生活の事象を定式化して数学的に考察する場面の設定をする必要があると考える。日常生活の事象と数学を結び付けて考察したり処理したりする活動を通して、数学を利用することの意義を実感させたり、既習の知識・技能、数学的な見方や考え方などの必要性を実感させたりすることが大切であると考える。
(イ)観察、操作や実験などの具体的な活動の充実
事象を観察して法則を見付けたり、具体的な操作や実験を試行錯誤し数学的な内容を帰納的に考えたりするなどして、数や図形の性質を見いだす学習活動を充実させる必要があると考える。
観察、操作や実験など具体的な活動において、予想を立ててその予想を記述し、それを確かめたり、その誤りに気付いて予想を見直したりする活動を取り入れることが大切であると考える。また、条件を変えて発展的に考え、予想する場合には、条件を変える前の学習内容に振り返って考えることができるようにすることも大切であると考える。既習の数学と結び付けたり、自分なりの方法で見いだしたりしていくような学習活動を取り入れていくことで、既習の数学の大切さに気付かせ、基礎的・基本的な知識・技能を身に付けさせたいと考える。
(ウ)説明し伝え合う学習活動の充実
生徒が学んだ数学を活用して考えたり判断したりすることをよりよく行うことができるよう、言葉や数、式、図、表、グラフなどの数学的な表現を用いて、論理的に考察し、表現したり、その過程を振り返って考えを深めたりする学習活動の充実させることが大切である。自分の考えを整理したり、表現を工夫したりして、相手に的確に分かりやすく伝えることで数学的な表現力が高まると考える。また、自分の考えをもち、説明し伝え合うことで、一人では気付かなかった新しい視点をもつことにもつながると考える。そのために、自分の考えを記述する場面を設定し、それを基に話し合ったり発表したりする活動を通して、数学的な用語を適切に用いた表し方を身に付けさせたい。数学的な表現を用いて説明する活動として、見いだした事柄や事実を説明すること、
事柄を調べる方法や手順を説明すること、
事柄が成り立つ理由を説明することの3つの場面を設定し、これらの活動を計画的・継続的に取り入れることによって数学的な見方や考え方を育てていきたいと考える。
○ 教師意識調査の結果より
教師意識調査(29)の「数学で、生徒が問題について、様々な考え方を出し合い、話し合っていくような活動を取り入れた授業を行っていますか。」という質問に対して、「多くの単元で行っている」と回答した教師の割合は、32.6%である。自分の考えを深めたり、新しい視点をもったりするためには、自分の考えを説明し伝え合う学習活動を充実させることが重要であると考える。そこで、1時間の授業の中で、ペアやグループで話し合って課題を解決するような場面を設定し、上記(ウ)の3つの数学的な表現を用いて説明する活動を充実させたいと考える。様々な考え方を出し合い、話し合っていくような活動を積み重ねることで、基礎的・基本的な知識・技能の定着を図ったり、数学的な見方や考え方を育てたりしていきたいと考える。 |
| |
|
| |
|
| オ |
授業実践に参考となるリンク |
| |
|
| |
 |
| |
|
| |
 |