過程 |
|
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
[問題]
下の平行四辺形ABCDの3倍の拡大図と、1/2の縮図をかきましょう。
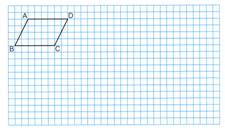
|
|
・ |
これまでの学習を振り返り、拡大図や縮図の性質を確認する。 |
・ |
前時の学習で、方眼を使って拡大図や縮図を見付けたことを想起させる。 |
|
方眼のます目を使って拡大図や縮図をかく方法を考えよう。 |
|
| 見通す |
| 2 |
解決の見通しをもつ。 |
| |
《予想される児童の考え》
・方眼のます目の数を数えてかく。
・辺の長さや角度をはかってかく。 |
|
・ |
斜めの線のかき方について話し合い、「右に○ます、上に□ます」と考えるとよいことを確認する。 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
| |
方眼を使って拡大図や縮図をかく。
|
|
| ◇ |
方眼を利用し、対応する辺の長さの比や角度の大きさに注意して拡大図や縮図をかかせる。 (ア) |
◎ 辺の長さや角の大きさに着目して、拡大図や縮図の意味を理解している。【知識・理解】(観察、ノート)
A 平行四辺形の辺の長さを3倍や1/2倍にし、斜めの辺は「右に○ます、上に□ます」と考えて作図し、作図した図の中に数値をかき込んで拡大図や縮図の性質を表している。
B 平行四辺形の辺の長さを3倍や1/2倍にし、斜めの辺は「右に○ます、上に□ます」と考えて作図している。
〔「努力を要する」状況(C)と判断した児童への指導〕
底辺の長さが3倍や1/2倍になるような底辺をかかせ、斜めの辺も「右に○ます、上に□ます」のように考えさせて作図させる。 |
| ※ |
学習活動の観察や授業後のノート記述の分析を基に、全員を対象とした評価を行い記録に残す。 |
|
| 学び合い |
|
| ◇ |
作図した図形が間違っていないか、拡大図や縮図の性質を振り返らせながら説明させる。(イ) |
|
5 |
考えたことをグループの代表が発表し、全体で話し合う。 |
| 《発表した児童の考え》 |
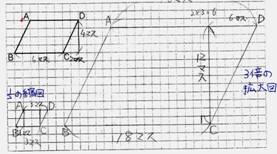

 |
| ◆ |
書画カメラを用いて児童のノートを拡大提示し、その図を使って作図の仕方を説明させる。 |
・ |
拡大図や縮図の作図には、拡大図や縮図の性質を利用していることを確認する。 |
|
| まとめる |
8 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際に書いた算数日記の例》 |


|
・ |
方眼のます目の数を数えて使うことにより、3倍の拡大図や1/2の縮図をかくことができたことを確認する。 |
○ 拡大図や縮図の性質を基に、拡大図や縮図をかいたり、対応する辺の長さや角の大きさを求めたりすることができる。 【技能】(ノート)
A 四角形ABCDは、四角形EFGHの1/2の縮図とも捉えられることに気付き、辺の長さを1/2倍して求めたり、角の大きさを求めたりすることができる。
B 四角形EFGHは、四角形ABCDの2倍の拡大図であることから、辺の長さを2倍して求めたり、角の大きさを求めたりすることができる。
〔「努力を要する」状況(C)と判断した児童への指導〕
対応する辺や角を見付けて印を付けさせ、対応する角の大きさは等しく、対応する辺の長さが2倍になることを確認する。 |
| ※ |
「努力を要する」状況(C)である児童が「おおむね満足できる」状況(B)となるよう指導し、本時において「十分満足できる」状況(A)になった児童がいれば記録に残す。 |
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|





