過程 |
|
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動(◎) |
|
つかむ |
[問題]
牛乳20mL、コーヒー50mLを混ぜて、コーヒー牛乳をつくりました。
どのような割合で混ぜたといえばよいですか。 |
|
| ○ |
実際に牛乳を入れた10mLカップ(2個)とコーヒーを入れた10mLカップ(5個)を並べて見せることで、比の表し方につなげる。 |
| ○ |
準備物…牛乳、市販のボトル入りコーヒー、
10mLカップ、プラスチックコップ(教師用) |
|
牛乳とコーヒーの量の割合を、2つの数を使って表す方法を考えよう |
|
見通す |
2 |
解決の見通しをもつ。 |
| |
《予想される児童の考え》
|
| |
① |
(比べる量)÷(基にする量)=(割合)
を使って考える。
|
| |
② |
10mLカップの個数を基に考える。 |
| |
③ |
かさで比べる。 |
|
| ◎ |
割合と比を関連付けさせるために、割合の考えを想起させる。(ア) |
| |
|
|
| 自力解決 |
3 |
自力解決をする。 |
| |
《予想される児童の考え》 |
| |
① |
牛乳を基にするとコーヒーは
50÷20=2.5 2.5倍
コーヒーを基にすると牛乳は
20÷50=0.4 0.4倍 |
| |
② |
牛乳は、10mLカップ2杯分
コーヒーは、10mLカップ5杯分 |
| |
③ |
牛乳とコーヒーは、20mLと50mL |
|
| ◎ |
割合で考える場合は、牛乳とコーヒーの関係を捉えさせるために、どちらを基として考えるかをはじめに考えさせる。(ア) |
| ◎ |
1つの方法で求めたら、他の方法も考えさせる。(ア) |
| ◎ |
この後の学び合いの活動で友達に説明させるために、ノートに図、式、言葉などを用いて記述するようにさせる。(イ) |
|
| 学び合い |
4 |
自分の考えをグループでお互いに説明し合う。 |
 |
「理由を明らかにして話し合っている様子」 |
|
| ◎ |
自分の考えを説明する際には、ノートを示しながら説明させる。(イ) |
| ◎ |
自分の考えを説明させる際には、児童が発言する次のような言葉に注目し、児童の考えをつなげていく。 (イ) |
| |
・まず…自分の考えを分割し、整理しようする言葉。
・でも…反例をあげ、考えを説明しようとする言葉。
・だったら…友達の考えを基にして、その先を考えて
説明しようとする言葉。
・もし…条件を変えたり、考えを整理したり、一般化
を図ったりしようとする言葉。 |
| ◎ |
これまでの学習を基に、言葉や図、式などを関連付けて説明させる。(イ) |
| ◎ |
自分のやり方と同じか違うかを意識させながら聞かせる。また、よく分からないところは、お互いに質問し合わせる。(イ) |
| ◎ |
説明を聞いて、自分の考えと異なる考えやよい考えがあったらノートにかかせる。(イ) |
◇ 割合の学習を基にして、牛乳とコーヒーの混ぜた割合を考えている。
【数学的な考え方】[ノート、行動観察] |
|
5 |
考えたことをグループの代表が発表・板書し、全体で話し合う。
|
| |
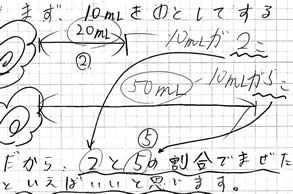
≪児童が実際にノートにかいた考え≫ |
|
|
|
◎ |
①、②、③の考えを関連付けることで、
割合の表し方と比の表し方をつなげる。(イ) |
| |
左の児童のノート例では、
牛乳が20mL、コーヒーが50mLであることを線分図で示している。(③の考え)それを牛乳は10mLカップ2杯分、コーヒーは10mLカップ5杯分と置き換えて考えている。(②の考え)
そして、「2と5の割合でまぜた」と表現している。
このことから、
牛乳 : コーヒー
2 : 5
という比の表し方へとつなげたいが、ここでは単元の導入であるため、
「20と50の割合でまぜた」とし、
牛乳 : コーヒー
20 : 50
という比の表し方へとつなげる。さらに、①の考えを取り入れ
「20は50の0.4倍である。」ことから、比の表し方を、割合の考えと関連付けて指導する。 |
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
・ |
比で表すと、牛乳 :コーヒー
20 : 50 となる。
|
| 7 |
本時の学習を算数日記にまとめる。 |
| ≪児童が実際に書いた算数日記の例≫ |
 |
|
| ○ |
比は、2つの数量を簡潔に表せるよさがあることを確認する。 |
◇ 比の意味と表し方を理解している。
【数量や図形についての知識・理解】[ノート、行動観察] |
|
| ○
|
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
|