過程 |
学 習 活 動 |
指導上の留意点(・)、評価規準と評価方法(◎○)
算数的活動(◇)、ICT利活用(◆) |
つかむ |
[問題]
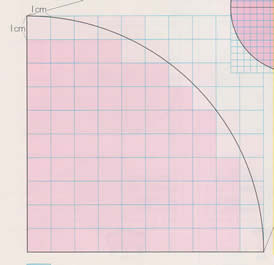
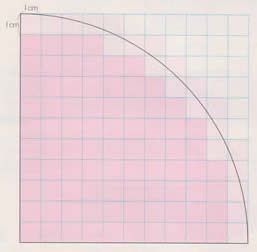
方眼を使って、半径10㎝の円のおよその面積を求めてみましょう。
 |
|
◆ |
電子黒板を用いて問題の図を提示し、課題を捉えさせる。 |
| |
|
・ |
これまでの面積の学習を想起させ、面積を求めるためには、単位となる正方形(1c㎡)がいくつあるかを調べればよいことに気付かせる。 |
| |
|
・ |
方眼を用いて、円の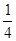 の面積を調べて、それを4倍すれば円全体の面積を求めることができることに気付かせる。 の面積を調べて、それを4倍すれば円全体の面積を求めることができることに気付かせる。 |
|
|
|
| 見通す |
|
・ |
円周の通っている方眼については、方眼の目をならして、どれも0.5c㎡と考えることを知らせる。 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
・ |
方眼の図を用いて円の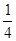 の面積を調べる。 の面積を調べる。 |
| |
|
| |
|
|
・ |
1c㎡の方眼の数は69こで69c㎡です。円周の通っている方眼の数は17こなので、その半分の8.5c㎡です。
だから、円の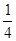 の面積は77.5c㎡。 の面積は77.5c㎡。
そして、その4倍が半径10㎝の円の面積なので、77.5×4=310で310c㎡になる。 |
|
◇
|
円の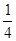 の方眼の数からおよその面積を求めて、4倍することで円全体の面積を求めさせる。 (ア) の方眼の数からおよその面積を求めて、4倍することで円全体の面積を求めさせる。 (ア) |
・ |
円周の通っている方眼とそうでない方眼を別々に数えさせる。 |
○ 方眼を用いて、円のおよその面積を求めることができる。【技能】(観察、ノート)
A 方眼の数を基に、円のおよその面積を式を用いて計算で求めることができる。
B 方眼の数を基に、円のおよその面積を求めることができる。
〔「努力を要する」状況(C)と判断した児童への指導〕
方眼に印を付けながら数えさせ、円周の通っている方眼はその半分と考えさせる。 |
| ※ |
「努力を要する」状況(C)である児童が「おおむね満足できる」状況(B)となるよう指導し、「十分満足できる」状況(A)の児童がいれば記録に残す。 |
|
| 学び合い |
|
・ |
方眼を用いて面積を調べたことについて説明し合う。 |
|
・ |
面積を調べたことを図や式や言葉などを用いて説明させる。 |
|
5 |
考えたことについて、全体で話し合う。 |
| |
|
・ |
半径を1辺とする正方形の面積の何倍の大きさになっているか考えさせる。 |
|
| ◇ |
円の面積を調べたことを基にして、半径10㎝の円の面積と、半径を1辺とする正方形の面積とを比較して何倍になっているか考えさせる。(イ) |
| ◆ |
書画カメラを用いて児童のノートを拡大提示し、それを使いながら説明させる。 |
・ |
正方形の面積は、半径×半径であることを確認する。 |
・ |
前時に学習した「円の面積は半径を1辺とする正方形の2倍より大きく4倍より小さい」ことと関連付けて、求めた結果(約3.1倍)がその範囲にあることを確認させる。 |
|
| まとめる |
6 |
本時の学習をまとめる。 |
| |
円の面積は、半径を1辺とする正方形の面積の約3.1倍になっている。 |
7 |
適用問題を解く。(教科書p5) |
| |
 |
| |
|
|
| |
|
|
| |
|
|
| 8 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際に書いた算数日記の例》 |
| |
|
|
・ |
円のおよその面積について、方眼を用いて調べることで、半径と面積の関係についてまとめることができたことを確認する。 |
| |
|
・ |
半径が11㎝の円の面積は、半径を1辺とする正方形の面積の何倍になっているか調べさせる。 |
・ |
調べて気付いたことをノートに記述させる。 |
◎ 円の面積は、半径を1辺とする正方形の面積の約3.1倍であることを理解している。
【知識・理解】(観察、ノート)
A 適用問題を解き、半径が10㎝の場合も半径が11㎝の場合も、円の面積は半径を1辺とする正方形の面積の約3.1倍になっていることから、どんな大きさの円でも約3.1倍になっているのではないかと類推し、そのことを記述している。
B 適用問題を解き、半径が11㎝の円の面積は半径を1辺とする正方形の面積の約3.1倍になっていることを記述している。
〔「努力を要する」状況(C)と判断した児童への指導〕
半径が10㎝の円の面積の求め方を想起させ、方眼の数え方や計算に誤りがないかを確認させる。 |
| ※ |
学習活動の観察や授業後のノート記述の分析を基に、全員を対象とした評価を行い記録に残す。 |
・ |
授業で分かったことや感想、これから気を付けたいことや更に調べてみたいことなどを書かせるようにする。 |
|



