|
|
研究の概要
|
(1) 研究テーマ |
知識・技能の習得を図り、数学的な思考力・判断力・表現力を育む学習指導の工夫
-数学的活動の充実を通して-
|
|
学習指導要領
から
|
学習指導要領では、
●基礎的・基本的な知識・技能を確実に身に付けること
●身に付けた知識・技能を活用して課題を解決する力を育成すること
が重視されています。
特に数学では、数学的な思考力・判断力・表現力を育成するために、
●根拠を明らかにして筋道を立てて体系的に考えること
●言葉や数、式、図、表、グラフなどの相互の関係を理解し、それらを適切に用いて
問題を解決すること
●自分の考えを分かりやすく説明すること
●互いに自分の考えを表現し伝え合ったりすること
などの指導を充実することが述べられています。
数学的活動は、
基礎的・基本的な知識及び技能を確実に身に付けるとともに、数学的に考える力を高めたり、数学を学ぶことの楽しさや意義を実感したりするために、重要な役割を果たすものです。
数学的活動は、一層の充実を図るために各学年の全領域を通して位置付けるようになっています。 |
| 全国学力・学習状況調査の結果から |
平成22年度の本調査における佐賀県採点分析委員会の報告によると、観点別では、B問題の「数学的な見方や考え方」に関する問題においての正答率が41.0%と、他の観点より低い結果となりました(表1)。
また、領域別で見ると、3領域すべてにおいてB問題の正答率が50%を下回る結果でした(表2)。
これらのことから、数学的な思考力・判断力・表現力及び身に付けた知識・技能を活用して課題を解決する力の育成を図っていくことが必要であると考えます。
| 表1 全国学力・学習状況調査の観点別正答率 (佐賀県) |
観 点 |
数学A |
数学B |
|
- |
41.0 |
|
65.5 |
73.2 |
数量、図形などについての知識・理解 |
61.6 |
- |
(平成22年4月20日実施) |
|
| 表2 全国学力・学習状況調査の領域別正答率 (佐賀県) |
領 域 |
数学A |
数学B |
数と式 |
75.3 |
44.5 |
図形 |
61.5 |
38.5 |
数量関係 |
53.3 |
45.6 |
(平成22年4月20日実施) |
|
さらに、下記の設問についての正答率と無解答率の結果から、特に、数量関係の領域における知識・技能の定着や、数学的な表現を用いて思考の過程や判断の根拠などを数学的に説明する力について、課題が見られました(表3)。
| 表3 全国学力・学習状況調査において課題が見られた設問の正答率と無解答率 |
| |
出題の趣旨 |
観点 |
領域 |
正答率 |
無解答率 |
数
学
A |
・円柱の体積の求め方を理解し、求めることができる
|
表現・処理 |
図形 |
35.4 |
19.4 |
・比例のグラフから、x の変域に対する y の変域を求めることができる |
表現・処理 |
数量関係 |
34.8 |
20.7 |
・具体的な事象における一次関数の関係を式で表すことができる |
表現・処理 |
数量関係 |
21.7 |
28.4 |
数
学
B |
・筋道立てて考え、事柄が一般的に成り立つ理由を説明することができる |
見方や
考え方 |
数と式 |
30.2 |
27.7 |
・事象を数学的に解釈し、問題解決の方法を数学的に説明することができる |
見方や
考え方 |
数量関係 |
27.9 |
26.5 |
・事象を数学的に解釈し、成り立つ事項の特徴を数学的な表現を用いて説明することができる |
見方や
考え方 |
図形 |
9.9 |
42.9 |
|
| 佐賀県小・中学校学習状況調査の結果から |
平成22年度佐賀県小・中学校学習状況調査について、Web報告書から、課題を取り上げてみます。
| ・ |
観点別では、「数量,図形などについての知識・理解」の正答率が、「おおむね達成」の基準を下回りました。理由の1つに、「球の体積」や「有効数字」等の学習内容の定着が十分でなかったことがあげられます。また、「数学的な見方や考え方」においては「おおむね達成」の基準をわずかに上回る結果にとどまり、「与えられた情報を読み取り、数学的に処理する力」などに課題が見られました。(図1) |
|
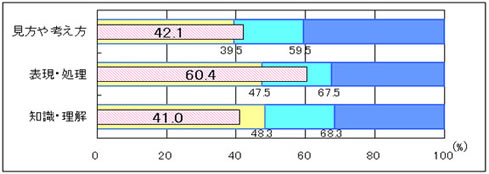
図1 H22年度 (中学2年生数学) 評価の観点別正答率
|
| ・ |
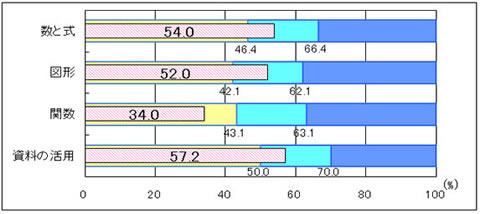
領域別では、「関数」の正答率が「おおむね達成」の基準を下回りました。理由として、「比例と反比例」に関する内容の定着が、十分でなかったことが考えられます。(図2) |
図2 H22年度 (中学2年生数学) 内容・領域別正答率
|
| ・ |
「活用」に関する記述式の問題において、正答率が「おおむね達成」の基準を下回り、しかも無解答率は30%を越える結果で、「数学的な表現を用いて、思考の過程や判断の根拠などを数学的に説明する力」に課題が見られました。(表4) |
表4 H22年度 (中学2年生数学) 記述式の問題の正答率・無解答率 |
問題
番号 |
出題のねらい |
正答率 |
無解答率 |
おおむね
達成 |
5(2) |
文字式を読み取り、説明することが
できる |
31.9 |
42.2 |
35.0
|
11(2) |
問題解決の方法を数学的に説明
することができる |
31.5 |
36.1 |
35.0
|
|
| |
|
| 研究の方針 |
このような、全国学力・学習状況調査や佐賀県小・中学校学習状況調査による佐賀県の実態や課題を踏まえながら、研究を進めていくことが大切であると考えます。
そして、知識・技能の習得を図り、数学的な思考力・判断力・表現力を育むためには、以下のような数学的活動を効果的に位置付け、授業の工夫を図る必要があると考えます。
●既習の数学を基にして、数や図形の性質を見いだし、発展させる活動
●日常生活や社会で数学を利用する活動
●数学的な表現を用いて根拠を明らかにし筋道立てて説明し伝え合う活動 |
|
| |
|
|
次の2つの視点から研究を進め、これからの数学科学習指導について提案していきます。 |
| |
|
ア 数学的活動を効果的に位置付けた授業展開案の作成 |
| |
教科書に沿った学習内容で、授業のねらいを達成するために、数学的活動を効果的に位置付けた授業プランを作成します。
①数学的活動を効果的に位置付けた授業展開案を第3学年の全単元分作成
②授業展開案を基に詳細授業展開案の作成
③詳細授業展開案の検証授業で利用するワークシートの作成
|
| |
|
イ 知識・技能の習得と数学的な思考力・判断力・表現力を育むための学習プリントの作成 |
| |
授業後の確認問題、宿題、単元末の問題、長期休業中の課題など、多様に利用できる学習プリントを3年生の内容で2種類作成します。
①学習指導要領の内容に示されている知識・技能の習得を図るための学習プリント
②根拠を明らかにし筋道を立てて体系的に考えたり、言葉や数、式、図、表、グラフなどの相
互の関係を理解し、それらを適切に用いて解決したりする学習プリント |
| |
|
|
| Copyright(C) 2011 SAGA Prefectural Education Center. All Rights Reserved. |
| |
|