| 採点の基準による比較 | ||||||||||
生徒の難しさを的確に把握するには,どのような基準で採点すればよいかを検討するために,採点の基準によって標準偏差及び平均点が,どのように変化するかを比較した。その結果,以下のようになった。
|
||||||||||
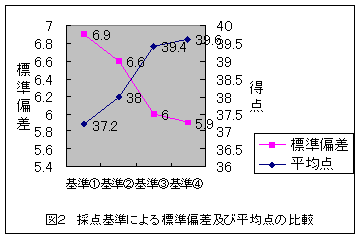 |
図2から・・・
|
|||||||||
| 中間テスト及び課題テストとの比較 | ||||||||||
| 学年集団として,今回の期末テストが取り組みやすいものとなったかどうかを見るために,標準偏差及び平均点を,中間テスト及び課題テストと比較した。その結果,以下のようになった。 | ||||||||||
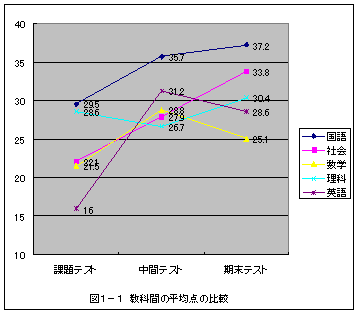 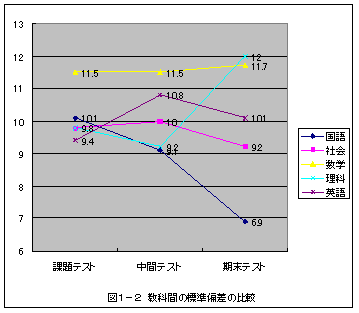 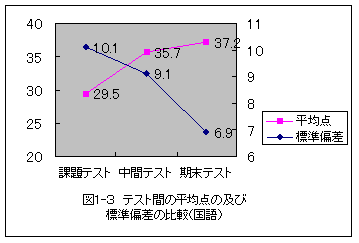 |
図1-1から・・・
図1-2から・・・
図1-3から・・・
これらのことから・・・
|
|||||||||