|
|
|
単元「三平方の定理」の小単元「三平方の定理」（３時間）における数学的活動を取り入れた授業展開案です。 |
| |
単元 三平方の定理 （啓林館）
１ 三平方の定理
【・１・ 三平方の定理】
全３時間
|
| |
| |
|
・ 直角三角形のそれぞれの辺を１辺とする３つの正方形の面積の関係について考えること
ができる。 |
| 段階 |
|
| つかむ |
| ○ |
教科書117ページの「とびらの問題」に取り組む。 |
| ○ |
かいた図が正しいか、グループで確認し合う。 |
| ○ |
本時の学習内容「直角三角形のそれぞれの辺を１辺とする３つの正方形の面積の関係について考えよう」を知る。 |
|
|
| 見通す |
| ● |
教科書118ページの「考えてみよう」に取り組む。 |
| ○ |
表に書き入れた値を確認し、表から気が付いたことを発表する。 |
|
| 練り合う |
| ● |
教科書117ページにかいた図について、P+Q =R が成り立つか確認する。 |
| ○ |
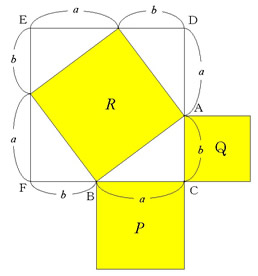
方眼紙に、直角三角形ABCの３辺を、それぞれ１辺とする正方形をかき、図のように、３つの面積をP、Q、R とする。△ABCと合同な直角三角形を、ABを１辺とする正方形の外側にかき加え、正方形EFCDをつくる。 (※ 方眼紙を準備する。)
|
| 数学的活動 〔目の前の課題から、物事の本質を見抜こうとする活動〕 |
| ● |
課題１を考える。
| BC＝a、CA＝b とするとき、面積R を a と b を使って表しましょう。 |
|
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループで、面積 R の式について、ノートの図を用いながら、自分の考えを説明し合う。 |
|
| 深める |
| ○ |
面積 R の式を計算する。 |
| ○ |
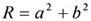を確認し、P+Q =R を理解する。
|
|
| まとめる |
| ● |
直角三角形のそれぞれの辺を１辺とする３つの正方形の面積の関係について、ノートにまとめる。 |
|
|
|
|
|
・ 三平方の定理を使って辺の長さを求めることができる。
・ 三平方の定理の意味を理解する。 |
| 段階 |
|
| つかむ |
| ○ |
本時の学習内容「三平方の定理を使って辺の長さを求めよう」を知る。 |
| ○ |
前時のまとめを基に、 |
 |
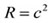を確認し、 |
 |
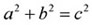を理解する。 |
|
|
| 見通す |
|
| 練り合う |
| ○ |
教科書120ページの例１と例２の説明を聞き、求め方を理解する。 |
| ○ |
教科書121ページの問１を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループで、辺の長さの求め方について、自分の考えを説明し合う。 |
| ○ |
答えを確認する。 |
|
| 深める |
| ● |
教科書122ページの練習問題①②③を考える。 |
| ○ |
練習問題①②③の答えを発表する。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループで、正方形のかき方について、自分の考えを説明し合う。 |
| ○ |
自分の考えを発表する。 |
| ○ |
答えを確認する。 |
|
| まとめる |
|
|
|
|
|
・ 三平方の定理の逆を使って直角三角形を見分けることができる。
・ 三平方の定理の逆の意味を理解する。 |
| 段階 |
|
| つかむ |
| ○ |
前時のまとめを基に、三平方の定理を確認する。 |
| ○ |
本時の学習内容「三平方の定理の逆を使って、直角三角形であるかどうかを調べよう」を知る。 |
|
|
| 見通す |
| ● |
教科書121ページの「考えてみよう」に取り組む。 |
|
| 練り合う |
| ○ |
三平方の定理の逆が成り立つことを理解する。
|
| ○ |
教科書122ページの問２を考える。 |
| 数学的活動 〔自分の考えを人に伝える活動・人の考えを理解する活動〕 |
| ● |
グループで、直角三角形であるかどうかについて、自分の考えを説明し合う。 |
| ○ |
答えを確認する。 |
|
| 深める |
| ● |
教科書122ページの練習問題⑤を考える。 |
| ○ |
自分の考えを発表する。 |
| ○ |
答えを確認する。 |
|
| まとめる |
|
|
|
| |
|
| Copyright(C) 2012 SAGA Prefectural Education Center. All Rights Reserved. |
|
