�ߒ� |
�w�K����
�Z���I���� |
�w����̗��ӓ_�i���j�A�]���K���ƕ]�����@�i���j
�Z���I�����̎w���ɂ�����闯�ӓ_�i���j |
���� |
�P�@�{���̉ۑ���Ƃ炦��B
�i���ȏ�15�y�[�W�̎O�p�`��p����B�j
�E�O�p�`�`�aC�̖ʐς����߂悤�B
�@�����狁�ߕ����l����B
�@�@�W�~�U���Q���Q�S(���u)
�@�@�u�W�~�U�v�͒����`�̖ʐ�
�@�@���Q�͂��̔���
�A�@�u�U���Q�v�͍����̔���
�@�@�䂦�ɁA�����̒����`�ɓ��ϕό`����
�@
�l������
�B�u�W���Q�v�͒�ӂ̔���
�@�@�䂦�ɁA�c���̒����`�ɓ��ϕό`����
�@
�l������
|
���@���Ɠ������o������B
���@������p�������u�W�~�U���Q�v�����グ�A���̈Ӗ����l��������B
���@������p���Ȃ��Ă����߂��鎮�����グ�A���̈Ӗ����l��������B
���@ �O���܂ł̊��K�������܂Ƃ߂��f�������Q�l�ɂ��Ȃ���A���̈Ӗ����l���Ă݂�悤�ɃA�h�o�C�X����B�B
�@�@�@
�@�@�u�w�K���e���ςݏグ��ꂽ�����f���v�@�@
|
|
|
�i���ȏ�15�y�[�W�̂����ь`��p����B�j
�E�����ь`�̐}�`�̖ʐς����߂悤�B
|
���@�ʐς̋��ߕ���������邽�߁A�}�Ǝ��Ɣ�ׂȂ���l��������B |
���ʂ� |
�Q�@�����̌��ʂ������B
�E���ߕ��̌��ʂ������B |
���@�ʐς̋��ߕ��̌��ʂ����������邽�߁A���K�̖ʐς̋��ߕ����f�����Ȃǂ���v���o������B
���@�P�ɖʐς����߂�̂ł͂Ȃ��A���Ɛ}���֘A�t���čl���A���̈Ӗ���ɐ����ł���悤�ɂ��邱�Ƃ��m���߂�B |
���͉��� |
�R�@���͉���������B �@
�����ь`�̖ʐς����߂�B
�s�\�z����鎙���̉t
�A�@�傫���O�p�`���珬�����O�p�`������
(�U�{�S)�~(�T�{�Q)���Q���R�T
(�U�{�S)�~�Q���Q���P�O
�R�T�|�P�O���Q�T
�C�@�Q�̎O�p�`������
���c�T�~�U���Q���P�T
�E�c�T�~�S���Q���P�O
�P�T�{�P�O���Q�T
�E�@�Q�̒��p�O�p�`�ɓ��ϕό`
���E�̎O�p�`�����ꂼ�꒼�p�O�p�`�ɕό`���čl����ƁA��ӂ�(�U�{�S)�ō������T�̐}�`�Ɠ����ʐςɂȂ�̂ŁA
(�U�{�S)�~�T���Q���Q�T
|
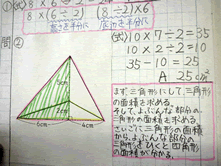
�u�A�̍l�����܂Ƃ߂������̃m�[�g�v |
���@�����ь`�̐}�`�̃��[�N�V�[�g��z�z���A������������A�������肷��Ȃǂ̍�ƓI�Ȋ����������A�ʐς����߂���@���l��������B�i�����̃��[�N�V�[�g��p�ӂ���B�j
���@�P�Ɏ������ŕ\���̂ł͂Ȃ��A����ɕ�����₷���`���邱�Ƃ��ӎ������A���߂�菇��\���A�}�⎮�A���t���֘A�t�����������l��������B
���@���߂鎮�̈Ӗ�����̓I�ɐ}�⌾�t�Ɗ֘A�t���đ���ɕ�����₷���`����悤�ɕ\��������B
���@�����ь`�̖ʐς����߁A���̋��ߕ���\�����Ƃ��ł���B
�y�\��������z
�k�s���ώ@�A�m�[�g�l |
���@�E�̐������ł��鎙���ɂ́A���t�̎����l���Ă݂�悤�ɑ����B
|
�w�э���
|
�S�@�����̍l�����y�A�Ő����������B
�E�����Ɠ����l����Ⴄ�l����
�E�ǂ̂悤�Ȏ��ɂȂ��Ă��邩
�E�ǂ̂悤�Ȑ}���g���Ă��邩 |
���@�߂��̗F�B�Ƃ��݂��̍l����`���������ƂŁA�����̍l����U��Ԃ点����A�������L�������肷��B
���@���Ɛ}��Ή������Ȃ������������B |
�T�@�����̍l����S�̂Ő����������B
�E�ǂ̂悤�ȕ��@�ŋ��߂��̂�
�E�ǂ����炻�̂��Ƃ�������̂�
�E�������߂鎮�Ȃ̂�
�E���ߕ��Ŏ��Ă���_�͉���
|
���@�l�����⋁�ߕ��Ȃǂ̐�����t�������Ȃ���S�̂ł̘b��������i�߂Ă����B
���@���͉����̃A�A�C�̏��ԂŘb���������s���A�E�ɂ��Ă͎����̔��\�ɉ����āA��舵�����Ƃɂ���B
���@�S�̂ł̘b�������ł́A�܂�������A���̎��̈Ӗ��i���l�̈Ӗ��A���̈Ӗ��Ȃǁj��}�`�Ɗ֘A�t���Ȃ���l�������A�ӌ����o�����킹�Ȃ���i�߂Ă����B
���@���݂��̍l���̋��ʓ_�⑊��_�Ȃǂ�b�����킹�钆�ł��ꂼ��̍l������F�߂Ȃ���A���̂悳�ɋC�t������B
���@�ʐς����߂鎮�̌`�ɒ��ڂ��A���̕\���Ӗ���}�`�Ɗ֘A�t���Ȃ���ǂݎ�邱�Ƃ��ł���B
�y���w�I�ȍl�����z
�k�s���ώ@�A�m�[�g�l�@ |
|
�܂Ƃ� |
�U�@�{���̊w�K��U��Ԃ�B
|
���@�ʐς̋��ߕ��ɂ���āA����}�Ȃǂ��قȂ邱�Ƃ��C�t������B
���@�{���̊w�K�ŁA����������Ƃ╪���������ƂȂǂɂ��ĐU��Ԃ点��B |
| |
�Q�l�����u�����̃m�[�g�v |
| |
|


