過程 |
学習活動
算数的活動 |
指導上の留意点（○）、評価規準と評価方法（◇）
算数的活動の指導にかかわる留意点（◎） |
つかむ |
１ 本時の課題をとらえる。
・台形ＡＢＣＤの面積を求める。
（補助教科書25ページの台形） |
○ 前時までの学習内容を振り返らせる。 |
|
|
見通す |
２ 解決の見通しをもつ。
・これまで学んだ公式を思い出して、面積を求める方法を見通す。 |
◎ 面積の求め方の見通しをもたせるため、既習の面積の求め方（三角形や平行四辺形で切り取ったり動かしたりして求めた方法）を掲示物などから思い出させた上で、どのような調べ方をすれば面積を求められるかを考えさせる。 |
自力解決 |
３ 自力解決をする。
台形の面積を求める。
《予想される児童の考え》
・三角形に分割
・三角形＋平行四辺形
・倍積変形（２つで平行四辺形）
|
自分の考えをまとめ表現する。
|
◎ 台形の図形のワークシートを配布し、線を引いたり、切り取ったり、動かしたりするなどの操作活動をさせ、面積を求める方法を考えさせる。
※ ワークシートは、そのまま提示して話し合えるように、拡大して使用する。（長さは、１ますを１cmとしてとらえさせて使用させる。）
◎ 単に式だけで表すのではなく、相手に分かりやすく伝えることを意識させ、求める手順を表し、図や式、言葉を関連付けた説明を考えさせる。
◇ 今まで学習した面積を求める方法を活用し、分割したリ結合したりして、台形の面積の求め方を考えることができる。
【数学的な考え方】
〔行動観察、ワークシート等〕
|
○ 考えることができた児童には、言葉の式を考えてみるように促す。
|
学び合い
|
４ ペアをつくり、お互いに自分の考えを説明し合う。
①図形の切り方･つなぎ方はどうか
②どのような図形と見て解いたか
|
◎ 近くの友達とお互いの考えを伝え合うことで、自分の考えを振り返ったり、情報の共有化を図ったりさせる。
◇ 既習の面積公式を基にして、台形の面積の求め方を進んで見いだそうとする。
【関心・意欲・態度】
〔行動観察、ワークシート等〕 |
|
５ 全体の場で、式と考えを説明する。
①三角形などに分割してたす考え
②倍積変形（平行四辺形と見る）
→倍積変形から台形の面積の公式につなげ、他
の考え方と比べ、共通性について振り返る。
・２つの方法から公式を考える。
|
◎ 考え方や解き方などの説明を付け加えながら全体での話し合いを進めていく。
◎ お互いの考えの共通点や相違点などを話し合わせる中で、それぞれの考え方を認めながら、そのよさに気付かせる。
○ 「台形を三角形２つ分と見た場合の面積を求める方法」と「台形２つ分で平行四辺形と見た場合の面積を求める方法」を取り上げ、２つの求め方の共通点を話し合わせ、台形の面積の公式へとつなげていく。
◇ 台形の面積の公式を理解できる。
【数量や図形についての知識･理解】
〔行動観察、ワークシート等〕
|
|
ま
と
め |
６ 本時の学習を振り返る。
|
７ 公式を使って練習問題を解く。
（補助教科書25ページの②番）
|
○ 上底と下底の用語を知らせる。
○ 底辺と高さにそれぞれ印を入れ全体で確認し、問題を解くようにする。 |
| |
参考資料「児童のノート」 |
| |
 
|
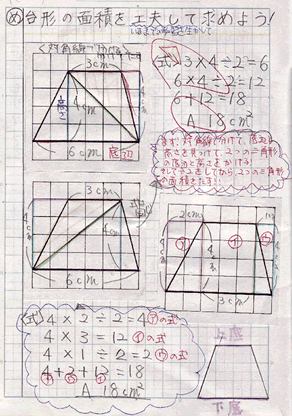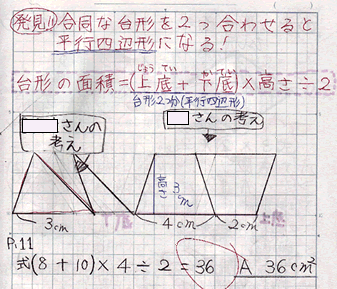
※ このワークシートは、作業用としてノートと併用します。