過程 |
学 習 活 動
(◎ 算数的活動) |
指導上の留意点(○)、評価規準と評価方法(◇)
算数的活動の指導にかかわる留意点(◎) |
つかむ |
| 1 |
今までの面積の単元の学習を振り返る。 |
| |
既習の面積の公式について確認する。 |
 |
| |
|
2 |
本時の問題を知り、課題をとらえる。 |
|
[問題]
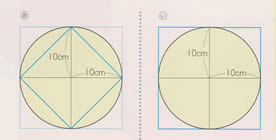
半径10㎝の円の面積について、下の図のように円の内と外に正方形をかいて、見当をつけてみましょう。
 |
|
| ○ |
長方形、三角形、平行四辺形などの図形の面積はそれぞれ公式を用いて求められることを想起させる。また、円についても面積を求められたことを知らせる。 |
| ○ |
円の面積については、マス目の大きさを細かくすることによって、単純に近似することが出来ることについてふれ、その求め方に関心がもてるようにする。 |
| |
|
| |
|
| ○ |
円のおよその面積の大きさに着目するようにさせる。 |
|
| 半径10㎝の円の面積について、見当をつけてみよう。 |
|
| 見通す |
|
| ○ |
円周の長さを直径の3倍よりも大きく4倍より小さいと見積もったことを想起させ、およその大きさを考えることの意味をとらえさせる。 |
|
| 自力解決 |
| 3 |
自力解決をする。 |
| ◎ |
円に内接する正方形と外接する正方形を利用して円の面積の見当付けをする。(ア) |
| |
《予想される児童の考え》
・1辺が10㎝の正方形のいくつ分かで考える。 |
|
| |
|
| ◎ |
円の面積は、円に内接する正方形と外接する正方形の間にあることから、およその円の面積について調べさせる。 (ア) |
|
| 学び合い |
4 |
自分の考えをグループや全体でお互いに説明し合う。 |
| ◎ |
円の面積は、半径1辺とする正方形の2倍と4倍の間にあることを説明する。(イ) |
|
・1辺が10㎝の正方形のいくつ分かで考えると、1辺が10㎝の正方形の2つ分より大きく、1辺が10㎝の正方形の4つ分より小さい。
(10×10)×2=200c㎡
(10×10)×4=400c㎡
だから、半径10㎝の円の面積は、
(10×10)×2より大きく(10×10)×4より小さい。 |
| 《児童が実際にノートにかいた考え》 |

|
| |
|
| |
|
| ◎ |
およその円の面積は、半径を1辺とする正方形で調べればよいことについて、式や図や言葉などを使って説明させる。(イ) |
| ○ |
面積は200c㎡と400c㎡の間にあることから、およそ300c㎡程であることを確認する。 |
◇ 正方形を使って、円の面積のおよその大きさの見当をつけようとしている。
【算数への関心・意欲・態度】[ノート、観察] |

|
| まとめる |
5 |
本時の学習をまとめる。 |
| |
円の面積は、半径を1辺とする正方形の面積の2倍より大きく、4倍より小さいことが分かる。 |
6 |
本時の学習を算数日記にまとめる。 |
| |
《児童が実際にノートにかいた算数日記》 |


|
| ○ |
円のおよその面積について、円を2つの正方形の面積の間にあることについて、見当を付けたことについてまとめる。 |
| |
|
| ○ |
授業で分かったことや感想、これから気を付けたいことやさらに調べてみたいことなどを書かせるようにする。 |
|




